Cantilever Beam: Moment and Shear Force Formulas Due To Different Loads

Calculating bending moments and shear forces in cantilever beams and other static systems for different loading scenarios is probably one of the things in structural engineering that we do throughout our studies and also careers later on.

While it’s very important to know how to derive and calculate the internal forces, the further we get in our studies, the more we can use beam moment and shear formulas.

After having covered the moment and shear formulas for simply supported beams in this article, we’ll show in this post, the most important and easiest formulas for cantilever beams due to different loading scenarios like UDL line loads, point loads, external moments and triangular loads.

All will be shown and explained by examples.

Now, before we get started, always remember that the unit of the bending moment is Kilonewton meter [$kNm$] and Kilonewton [$kN$] for the shear forces when in Europe.

But now, let’s get started.

1. What is a Cantilever beam?

A cantilever is a static system acting as a beam in bending and shear. Therefore, it is also called a cantilever beam. It is characterized by having only one support – a fixed – on one end and no support on the other.

But where are cantilever beams actually used? Well quite a lot, let’s have a look.

Here are 10 examples of cantilever beams represented in “real” structures

• Balconies
• Traffic light posts and systems cantilevering over the street
• Overhangs of roofs
• Construction of bridges with the balanced cantilever method
• Balconies
• Aeroplane wings
• Side mirrors on a car
• High-rise buildings (vertical cantilevers)
• Bookshelves attached to the wall
• Cranes
• Wind turbine blades

You can read up more in depth here. We have written an extensive article about cantilever beams.

2. Cantilever beam – uniformly distributed line load (UDL) formulas

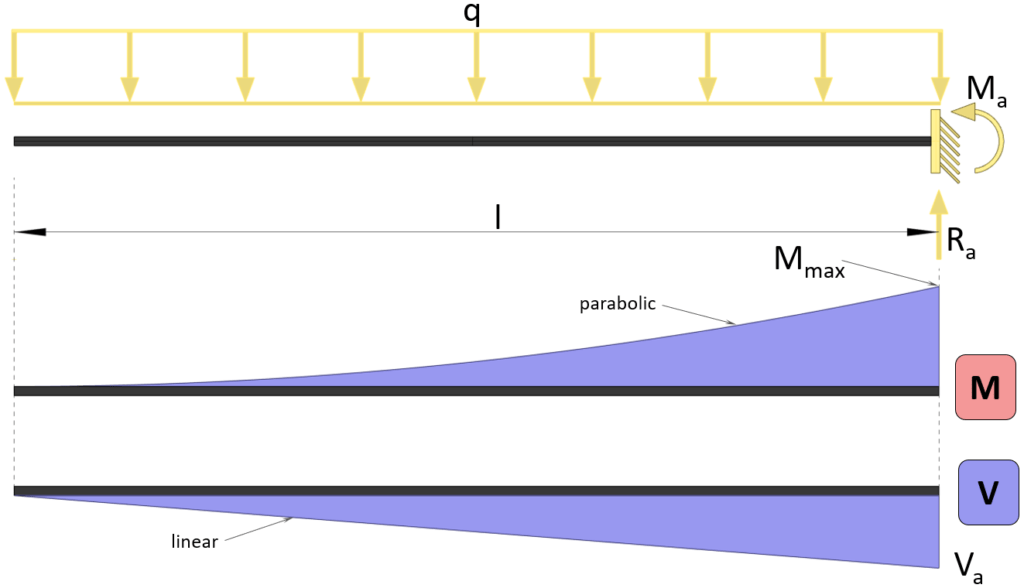
Bending moment

$M(x) = -1/2 \cdot q \cdot x^2$

Max bending moment

$M_{max} = -1/2 \cdot q \cdot l^2$

Shear force at support

$V_{a} = -q \cdot l$

Reaction forces

$R_a = q \cdot l$

Those formulas can also be calculated by hand. Check out this article if you want to learn in depth how to calculate the bending moments, shear and reaction forces by hand.

3. Cantilever beam – Point load at free end (formulas)

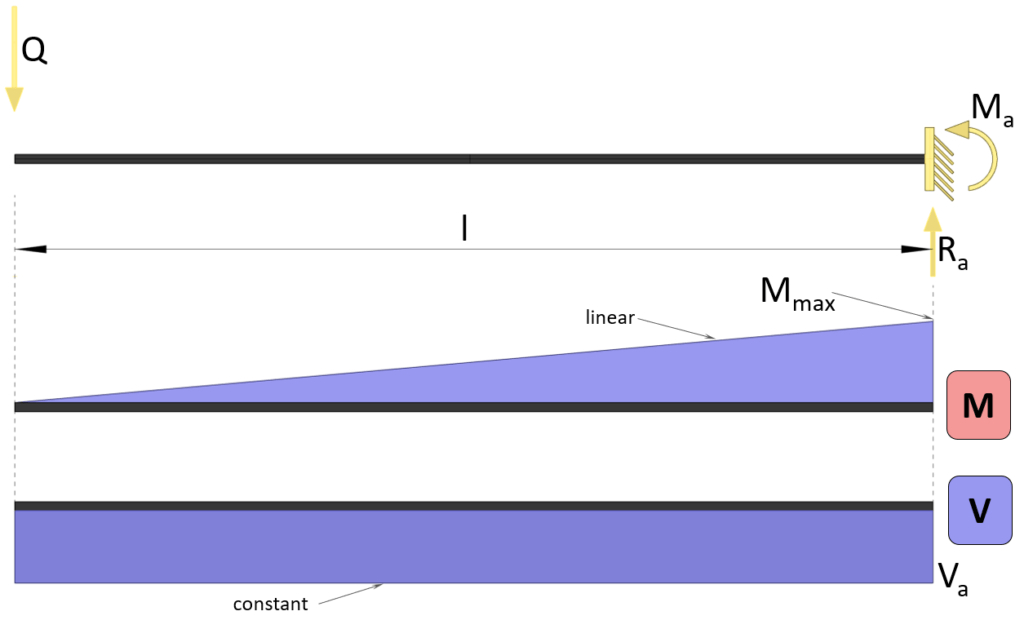
Bending moment

$M(x) = -Q \cdot x$

Max bending moment

$M_{max} = -Q \cdot l$

Shear forces at supports

$V_{a} = -Q$

Reaction forces

$R_{a} = Q$

4. Cantilever beam – Intermediate Point load (formulas)

Bending moment

$M(x) = -Q \cdot (a-x)$  if 0<x<a

$M = 0$ if x>a

Max bending moment

$M_{max} = -Q \cdot a$

Shear forces at supports

$V_{a} = -Q$

Reaction forces

$R_{a} = Q$

5. Cantilever beam – 2 Point loads (formulas)

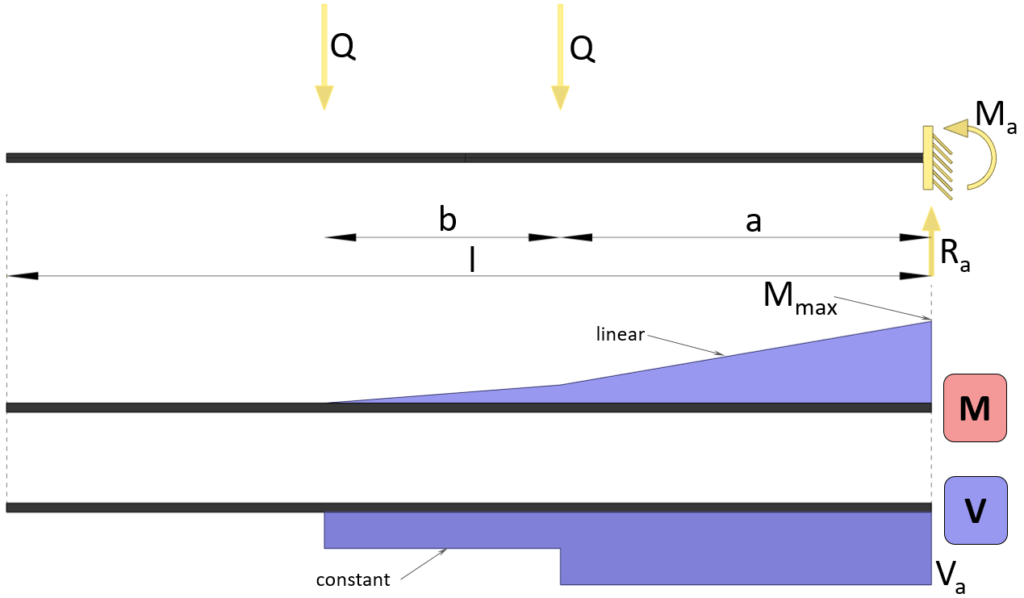
Max bending moment

$M_{max} = -Q \cdot a – Q\cdot (a+b)$

Shear force at support

$V_{a} = -(Q+Q) = -2Q$

Reaction force

$R_{a} = Q+Q = 2Q$

6. Cantilever beam – 3 Point loads (formulas)

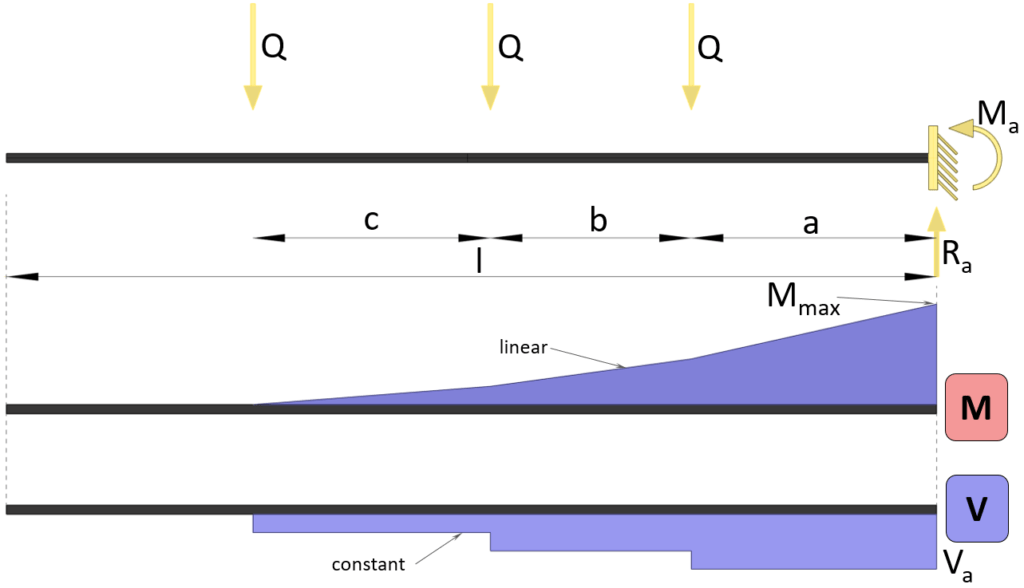
Max bending moment

$M_{max} = -Q \cdot a – Q\cdot (a+b) – Q\cdot (a+b+c)$

Shear force at support

$V_{a} = -(Q+Q+Q) = -3Q$

Reaction force

$R_{a} = Q+Q+Q = 3Q$

7. Cantilever beam – Triangular load (formulas)

Bending moment

$M(x) = -1/6 \cdot q \cdot \frac{x^3}{l}$

Max Bending moment

$M_{max} = -1/6 \cdot q \cdot l^2$

Shear force at support

$V_{a} = -1/2 \cdot q \cdot l$

Reaction forces

$R_{a} = 1/2 \cdot q \cdot l$

8. Cantilever beam – External moment (formulas)

Bending moment

$M(x) = -M$

Max Bending moment

$M_{max} = -M$

Shear force

$V_{x} = 0$

Reaction forces

$R_{a} = 0$

---

If you are new to structural design, then check out our design tutorials where you can learn how to use the calculated bending moments and shear forces to design structural elements such as

• Design of timber roof beams
• Buckling design of timber columns
• Buckling design of the collar beam

Do you miss any Moment or shear force formulas for the cantilever beam that we forgot in this article? Let us know in the comments✍️