Rigid Frame Structure: Moment formulas – Different loads
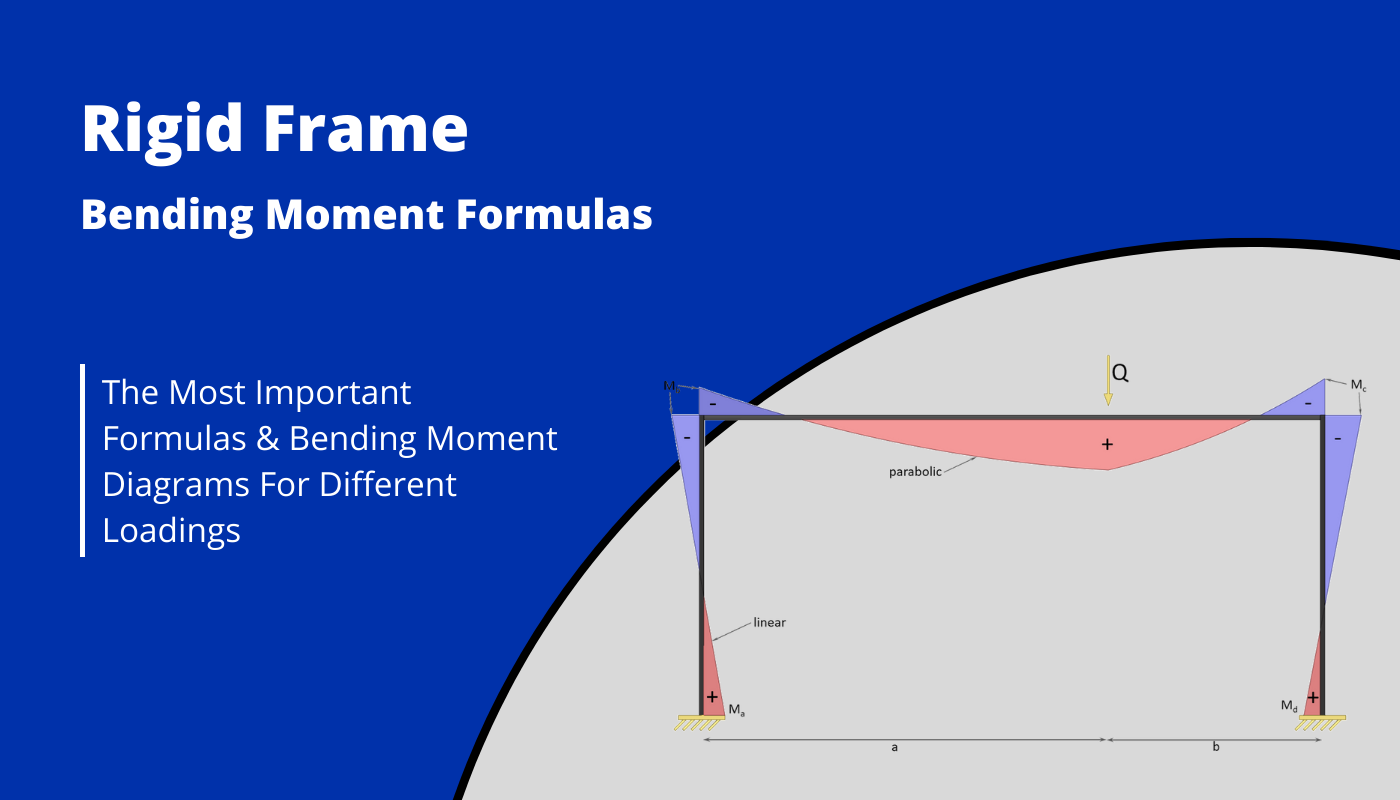
Calculating bending moments in structural elements – in this case rigid frames with two fixed supports – for different loading scenarios, is probably one of the things in structural engineering that we do throughout our studies and also careers later on.
While it’s very important to know how to derive and calculate reaction and internal forces, the further we get in our studies, the more we can use frame moment formulas.
In earlier articles, we already covered moment and shear force formulas and diagrams for:
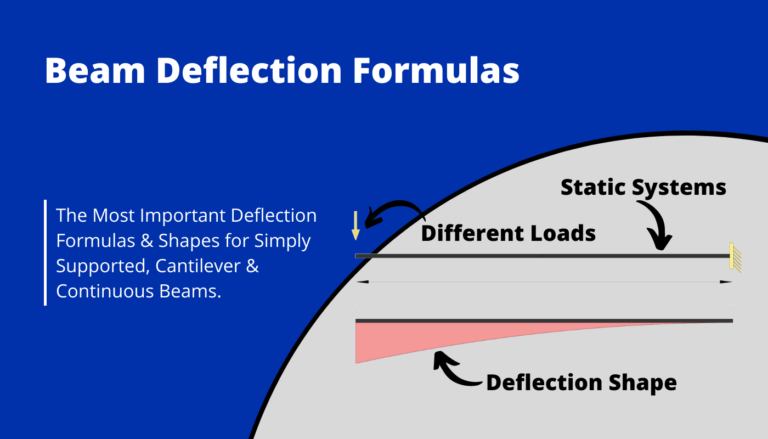
- Simply supported beams
- Cantilever beams
- 2 span continuous beams
- 3 span continuous beams
- 4 span continuous beams
In this article, we’ll show, the most important and easiest Moment formulas for frames with 2 fixed supports due to different loading scenarios like UDL line loads, point loads and external moments.
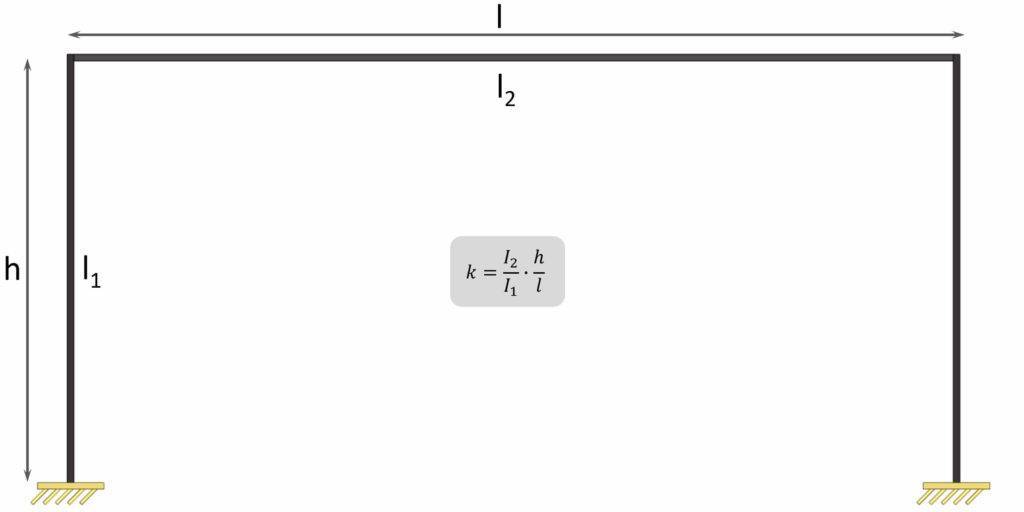
Before we start, some boundary conditions are set, such as that
- the 2 columns have the same Moment of inertia $I_1$ and a length of h
- the top beam has the Moment of inertia $I_2$ and a length of l
- the parameter k is defined as $\frac{I_2}{I_1} \cdot \frac{h}{l}$.
1. Uniformly distributed line load (UDL) on beam
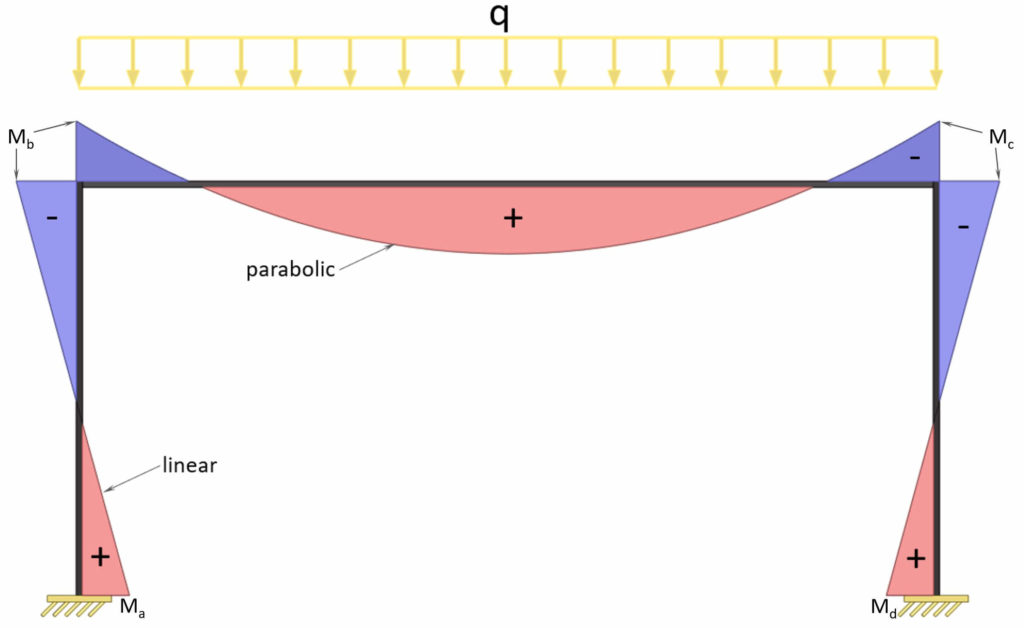
Moment (support a & d)
$M_a = M_d = \frac{q \cdot l^2}{12\cdot (k+2)}$
Moment (b & c)
$M_b = M_c = -\frac{q \cdot l^2}{6\cdot (k+2)}$
2. Uniformly distributed load (UDL) on both columns

Moment (support a & d)
$M_a = M_d = – \frac{1}{12} \cdot q \cdot h^2 \cdot \frac{k+3}{k+2}$
Moment (b & c)
$M_b = M_c = – \frac{1}{12} \cdot q \cdot h^2 \cdot \frac{k}{k+2}$
3. Uniformly distributed load (UDL) on 1 column
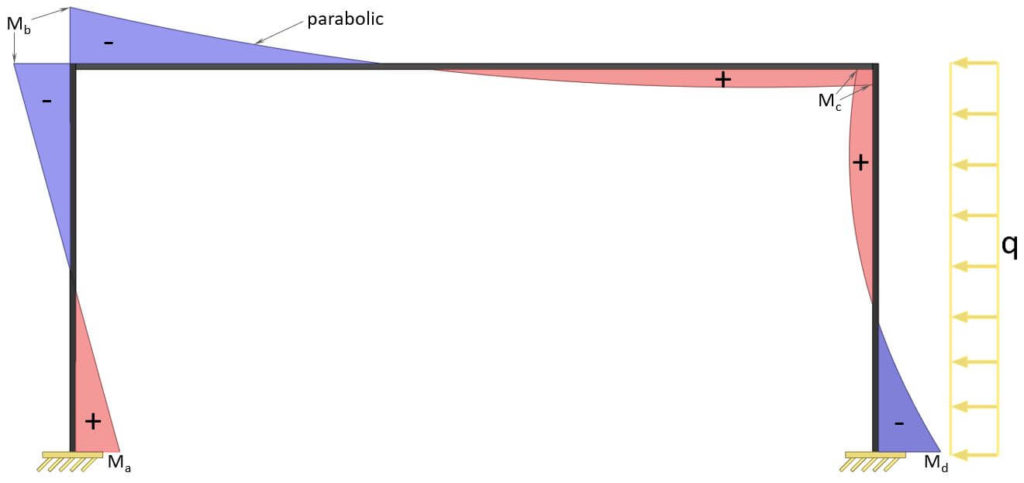
Moment (support a)
$M_a = \frac{1}{24} \cdot q \cdot h^2 \cdot (\frac{5k+9}{k+2}-\frac{12k}{6k+1})$
Moment b
$M_b = – \frac{1}{24} \cdot q \cdot h^2 \cdot (\frac{12k}{6k+1}+\frac{k}{k+2})$
Moment c
$M_c = \frac{1}{24} \cdot q \cdot h^2 \cdot (\frac{12k}{6k+1}-\frac{k}{k+2})$
Moment (support d)
$M_d = – \frac{1}{24} \cdot q \cdot h^2 \cdot (12 – \frac{5k+9}{k+2} – \frac{12k}{6k+1})$
4. Point load on beam
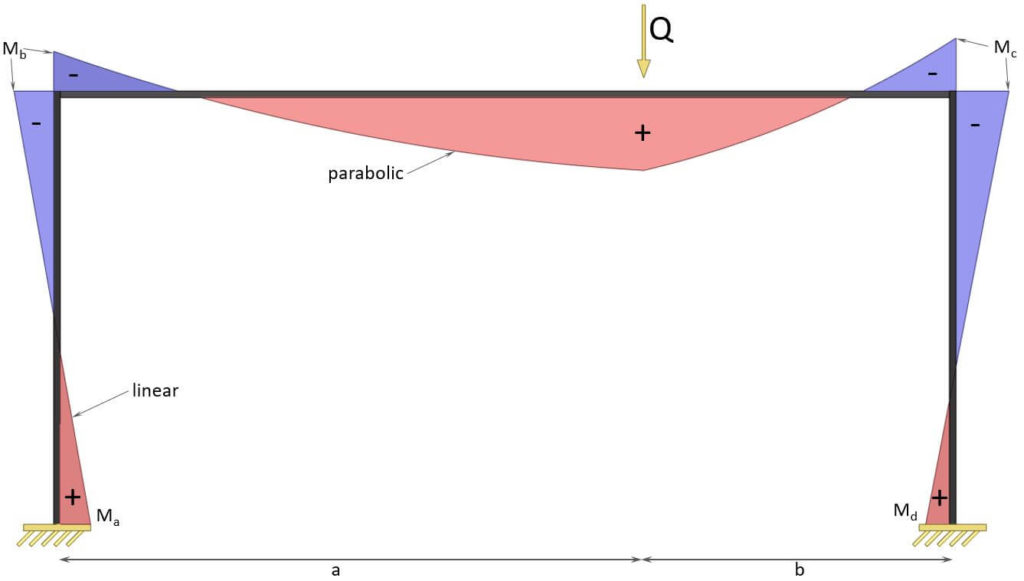
Moment (support a)
$M_a = \frac{Q\cdot a \cdot b}{2\cdot l} \cdot \frac{5k-1+2\cdot(k+2)\cdot \frac{a}{l}}{(k+2)\cdot(6k+1)}$
Moment b
$M_b = – \frac{Q\cdot a \cdot b}{2\cdot l} \cdot \frac{13k+4-2\cdot(k+2)\cdot \frac{a}{l}}{(k+2)\cdot(6k+1)}$
Moment c
$M_c = – \frac{Q\cdot a \cdot b}{2\cdot l} \cdot \frac{11k+2\cdot(k+2)\cdot \frac{a}{l}}{(k+2)\cdot(6k+1)}$
Moment (support d)
$M_d = \frac{Q\cdot a \cdot b}{2\cdot l} \cdot \frac{7k+3-2\cdot(k+2)\cdot \frac{a}{l}}{(k+2)\cdot(6k+1)}$
5. Point load on Column
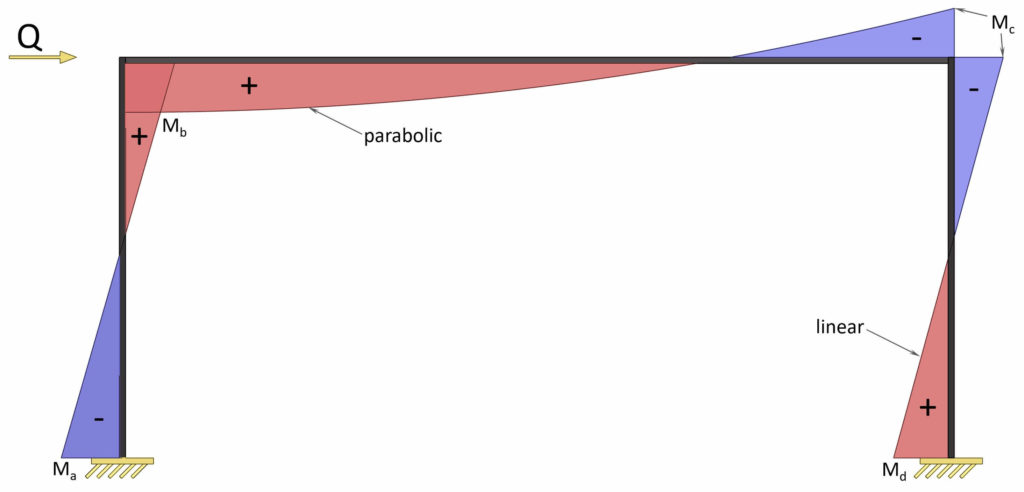
Moment (support a & d)
$M_a = -M_d = – \frac{1}{2} \cdot Q \cdot h \cdot \frac{3k+1}{6k+1}$
Moment (b & c)
$M_b = -M_c = \frac{1}{2} \cdot Q \cdot h \cdot \frac{3k}{6k+1}$
If you are new to structural design, then check out our design tutorials where you can learn how to use the calculated bending moments and shear forces to design structural elements such as
Do you miss any formulas for this rigid frame that we forgot in this article? Let us know in the comments✍️
![Understand Bending Moments [Everything YOU Need To Know – 2025]](https://www.structuralbasics.com/wp-content/uploads/2023/05/Bending-moment-768x439.jpg)