How To Calculate The Peak Velocity Pressure {2025}

The calculation of the peak velocity pressure is the 1st step when calculating the wind load on roofs, walls and bridges. 💨🌬️

In this blog post we show, step-by-step, how to calculate the peak velocity pressure according to Eurocode. 🧮🔢

Before we start calculating anything, let’s start with the question: What do we need the peak velocity pressure for? 🤔🤔

The value of the peak velocity pressure includes many parameters about the location, height of the building and some more. The unit is in $kN/m^2$, and we need the peak velocity pressure to calculate the wind forces which act on roofs and facades/walls.

Let’s get started. 🚀🚀

Process of peak velocity pressure calculation

To calculate the peak velocity pressure, we have to do the following steps. 👇👇

1. Geometry of the structure

As you might have already figured out – I like to use examples. This time, we will calculate the peak velocity pressure for a precast concrete office building. The material does not matter for this calculation. We need the dimensions of the building.

As you can see from the picture, the building has the following dimensions

Height above ground

z = 17.1m

2. Fundamental value of basic wind velocity v_b.0

According to EN 1991-1-4 1.6.1 the fundamental value of basic wind velocity describes a 10-minute mean value at a height of 10 m above ground and in an open country terrain which includes annual risks and some more parameters.

For the exact definition, you can have a look at the mentioned Eurocode section.

This value must be found in the Nation Annex

Or: We can also use the wind speed calculator made by Dlubal Software GmbH.  Click here to open the online calculator. 👇👇

1. Step: Click on the wind icon

2. Step: Choose your country and national annex

3. Step: Type in the location of the structure

Btw, Østerbro is the district in Copenhagen in which I live. ✌️😄

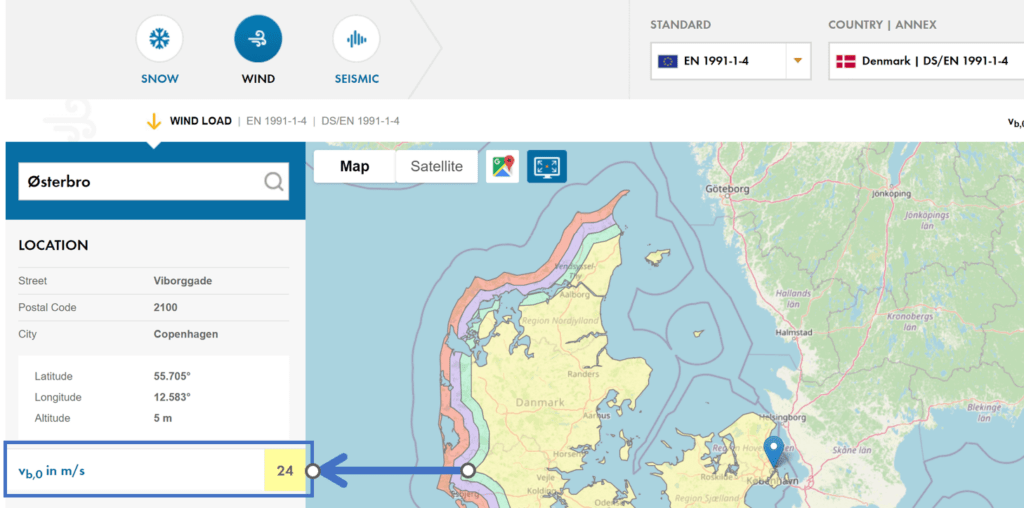
For an office building located in Copenhagen, Denmark, we get a fundamental value of the basic wind velocity of

$$v_{b.0} = 24 \frac{m}{s}$$

3. Orography factor c₀

EN 1991-1-4 4.3.1 (1) recommends the Orography factor to be taken as 1.0.

$$c_{0} = 1.0 $$

4. Turbulence factor k_l

As for the Orography factor, EN 1991-1-4 4.4 (4.7) recommends also the turbulence factor to be takes as 1.0.

$$k_{l} = 1.0 $$

5. Density of air $\rho$

The recommended value for the density of air is given in EN 1991-1-4 4.5 (1) and it is 1.25 kg/m³.

$$\rho = 1.25 \frac{kg}{m^3}$$

6. Reference height Terrain category II z_0.II

The reference height of terrain category II is used to calculate the terrain factor k_r. The value can be found in EN 1991-1-4 Table 4.1.

$$z_{0.II} = 0.05 m$$

7. Roughness Length z₀

The roughness length is also used to calculate the terrain factor k_r.

The value depends on the terrain category where our building or structure is located. The value can also be found in EN 1991-1-4 Table 4.1.

In our case, we assume that our office building is located in a suburban terrain with regular cover of buildings.

Therefore, the building falls into terrain category III.

$$z_{0} = 0.3 m$$

8. Terrain factor k_r

The formula to calculate can be found in EN 1991-1-4 (4.5).

$$k_{r} = 0.19 \cdot (\frac{z_{0}}{z_{0.II}})^{0.07}$$

Inserting the values of $z_{0.II}$ and $z_{0} $ leads to

$$k_{r} = 0.19 \cdot (\frac{0.3m}{0.05m})^{0.07} = 0.215$$

9. Turbulence Intensity I_v

The turbulence intensity is calculated with EN 1991-1-4 (4.7).

$$I_{v} = \frac{k_{1}}{c_{0} \cdot ln(\frac{z}{z_{0}})}$$

leading to

$$I_{v} = \frac{1.0}{1.0 \cdot ln(\frac{17.1m}{0.3m})} = 0.247$$

10. Roughness factor c_r

The roughness factor is calculated with EN 1991-1-4 (4.4)

$$c_{r} = k_{r} \cdot ln(\frac{z}{z_{0}})$$

leading to

$$c_{r} = 0.215 \cdot ln(\frac{17.1}{0.3m}) = 0.871$$

11. Seasonal factor c_season

The principle of the seasonal factor is that the wind load can be lowered because the wind is blowing less strong in some months.

In the case that you are designing a temporary structure such as a tent or a canopy that is built for a short time frame and then disassembled after a few weeks, you might be able to use a seasonal factor c_season depending on the months it has to withstand the wind.

When you need to design your structure for the execution phase, then you might also be able to use c_season. We are designing an office building which is NOT temporary and therefore c_season is taken as 1.0 and can be left out of the calculations.

$$c_{season} = 1.0$$

12. Directional factor c_dir

The principle of the directional factor is that the wind is blowing less from certain directions and therefore the peak velocity pressure and then the wind load can be reduced for those directions.

The recommended value for the directional factor is given in EN 1991-1-4 4.2 Note 2 as 1.0.

However, it is also referred to the National annex, which might define c_dir.

$$c_{dir} = 1.0$$

In further calculations, c_dir is not included because a value of 1.0 is neither increasing nor decrease the peak velocity pressure.

13. Mean wind velocity v_m

The mean wind velocity is calculated by EN 1991-1-4 (4.3) as

$$v_{m} = c_{r} \cdot c_{0} \cdot v_{b.0}$$

leading to a mean wind velocity of

$$v_{m} = 0.871 \cdot 1.0 \cdot 24 \frac{m}{s} = 20.9 \frac{m}{s}$$

Finally, we can calculate the peak velocity pressure. 👍👍

14. Peak velocity pressure q_p

The mean wind velocity is calculated by EN 1991-1-4 (4.8) as

$$q_{p} = [1 + 7 \cdot I_{v}] \cdot \frac{1}{2} \cdot \rho \cdot v_{m}^2$$

leading to a peak velocity pressure of

$$q_{p} = [1 + 7 \cdot 0.247] \cdot \frac{1}{2} \cdot 1.25\frac{kg}{m3} \cdot (20.9 \frac{m}{s})^2 = 0.746  \frac{kN}{m^2}$$

Summary

For a building with the height of 17.1 m in a suburban area in Copenhagen, Denmark, the wind load can be calculated with a peak velocity pressure of q_p = 0.746 kN/m².

And that is exactly what we did in the following articles: 👇👇

• Wind load calculation of walls
• Wind load calculation of a flat roof
• Wind load calculation of a pitched roof
• Wind load calculation of an arched structure

Peak Velocity Pressure FAQ