Wind Loads On A Pitched Roof {A Structural Guide}

Wind loads on roofs need to be considered in the structural design of every building.

In this article, I show you how I as a structural engineer calculate the wind loads on pitched roofs according to EN 1991-1-4.

This article builds up on the peak velocity pressure, which we calculated in a previous article for a precast office building.

We don’t repeat the calculation in this article, but define a value q_p for it.

Just keep in mind that the values differ due to different parameters such as location and geometry.

Let’s get started.

Step-By-Step Process Of Calculating The Wind Loads On Pitched Roofs

In order to calculate the wind load or wind pressure on external surfaces of a pitched roof, we are going to do the following steps:

Example Building

We’ll use the following example building with a rafter roof to show step-by-step how to calculate the wind load on a pitched roof.

Geometry and Parameters From Wind Velocity Pressure

This is a quick summary of the values we calculate to get the wind velocity pressure. As already explained earlier, check out this article, if you want to learn how to calculate these parameters.

Height of the building above ground	h	6.0 m
Fundamental value of basic wind velocity	vb.0	24 m/s
Orography factor	c0	1.0
Turbulence factor	kl	1.0
Density of air	$\rho$	1.25 kg/m3
Reference height of terrain cat. II	z0.II	0.05 m
Roughness Length (Terrain cat. III)	z0	0.3 m
Terrain factor	kr	0.215
Turbulence Intensity	Iv	0.334
Roughness factor	cr	0.65
Mean wind velocity	vm	15.5 m/s
Peak velocity pressure	qp	0.5 kN/m2

Wind Pressure on Roof Surfaces

Eurocode (EN 1991-1-4:2005) distinguishes in general between wind pressure on external and internal surfaces. This article is focusing on the wind pressure on external surfaces.

Wind pressure on external pitched roof surfaces w_e

Now we have written the exact same words and formulas already in the articles about the wind load of the flat roof and walls, but isn’t it good to repeat things, so they stick better with us? 🤔

Anyway, the formula (EN 1991-1-4:2005 (5.1)) to calculate the wind pressure on external surfaces is:

Where

qp	is the peak velocity pressure and
cpe	is the external pressure coefficient

The coefficient c_pe has 2 different values depending on the wind loaded area. There is a value for a surface area of 1 m² and 10 m². These two values can also be written as

cpe.1	for the external pressure coefficient for an area of 1 m2 and
cpe.10	for the external pressure coefficient for an area of 10 m2

Now, we already explained it a bit more detailed here. If you want to a more detailed explanation then either go to the article or read up in EN 1991-1-4:2005 7.2.

EN 1991-1-4 Table 7.3a and Table 7.3b give recommendations for c_pe.10 and c_pe.1.

Tables 7.3a and 7.3b give values for 4 different areas F, G, H and I of our roof. Those areas depend on where the wind comes from and the shape of the roof.

Eurocode differentiates between mono- and duo pitched roofs.

What are mono- and duopitched roofs?

A mono pitched roof has basically only “one slope”. So no change in slope.

The duo pitch roof has basically “two slopes” which change at the highest point of the roof.

For “our” duo pitched roof, we can define the areas for both wind directions – Wind from the front and from the side.

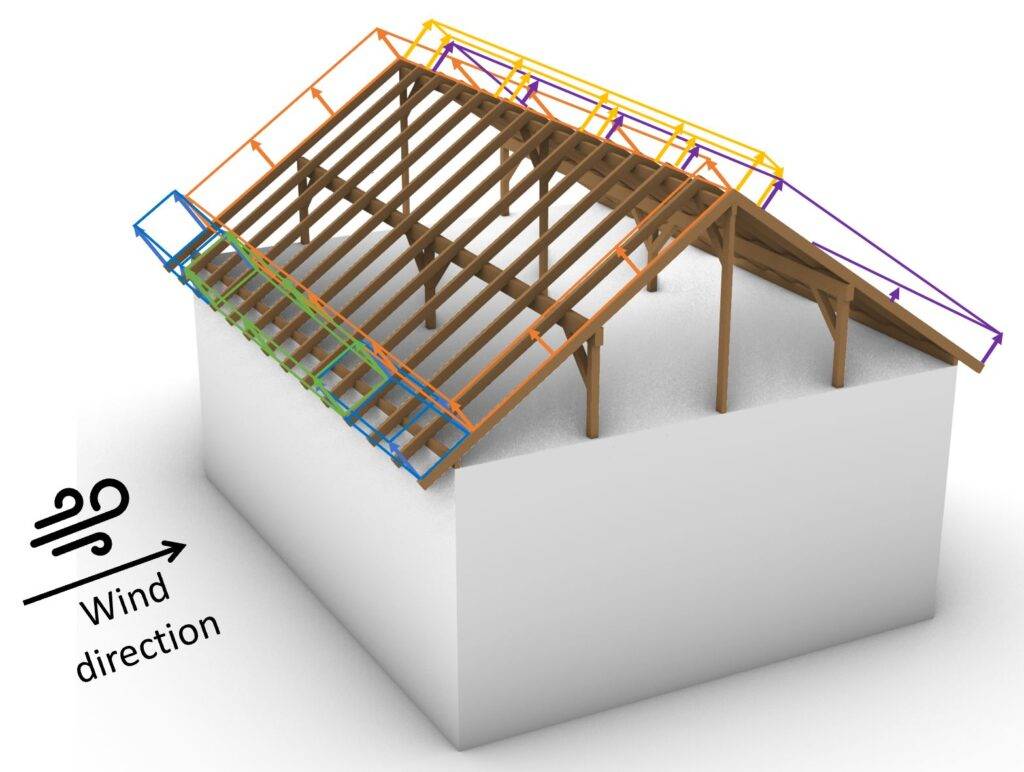
Wind directions

We will be talking about wind from front and side in this article. The following picture emphasizes what we mean by front and side.

Wind from Front

For the case that the wind blows from the front direction, we can define some geometric dimensions of the building according to EN 1991-1-4:2005

Width of building	b	13.0 m
Length of building	–	9.0 m
Height of building	h	6.0 m

From those dimensions we can define e which determines the widths and depths of Areas F, G, H, J and I according to EN 1991-1-4:2005 Figure 7.8.

$$e = min(b, 2h)$$

$$e = min(13.0m, 2 \cdot 6.0m=12.0m) = 12.0m$$

From e we get the dimensions of the areas according to EN 1991-1-4:2005 Figure 7.8.

Area	Width	Depth
F	e/4 = 3.0m	e/10 = 1.2m
G	b-e/2 = 7.0m	e/10 = 1.2m
H	b = 13.0m	Ridge depth – e/10 = 3.3m
J	b = 13.0m	e/10 = 1.2m
I	b = 13.0m	Ridge depth – e/10 = 3.3m

So many numbers – I know. Let’s visualize them.

Okay, now let’s go back to the formula for the wind pressure for external surfaces and derive the values. The peak velocity pressure was calculated as:

The external pressure coefficients for duopitch roofs with wind from front (direction angle $\Theta$) can be taken from EN 1991-1-4:2005 Table 7.4a.

For a roof slope angle of 29° $\approx$ 30° we get

Area	cpe.10	cpe.1
Area F	-0.5/0.7	-1.5/0.7
Area G	-0.5/0.7	-1.5/0.7
Area H	-0.2/0.4	-0.2/0.4
Area I	-0.4/0	-0.4/0
Area J	-0.5/0	-0.5/0

Based on our coefficients, we can now calculate the wind pressure on external surfaces.

Area	we.10	we.1
Area F	$-0.5(/0.7) \cdot 0.5 \frac{kN}{m^2} = -0.25(/0.35) \frac{kN}{m^2} $	$-1.5(/0.7) \cdot 0.5 \frac{kN}{m^2} = -0.75(/0.35) \frac{kN}{m^2}$
Area G	$-0.5(/0.7) \cdot 0.5 \frac{kN}{m^2} = -0.25(/0.35) \frac{kN}{m^2} $	$-1.5(/0.7) \cdot 0.5 \frac{kN}{m^2} = -0.75(/0.35) \frac{kN}{m^2}$
Area H	$-0.2(/0.4) \cdot 0.5 \frac{kN}{m^2} = -0.1(/0.2) \frac{kN}{m^2} $	$-0.2(/0.4) \cdot 0.5 \frac{kN}{m^2} = -0.1(/0.2) \frac{kN}{m^2}$
Area I	$-0.4(/0.0) \cdot 0.5 \frac{kN}{m^2} = -0.2(/0.0) \frac{kN}{m^2} $	$-0.4(/0.0) \cdot 0.5 \frac{kN}{m^2} = -0.2(/0.0) \frac{kN}{m^2}$
Area J	$-0.5(/0.0) \cdot 0.5 \frac{kN}{m^2} = -0.25(/0.0) \frac{kN}{m^2} $	$-0.5(/0.0) \cdot 0.5 \frac{kN}{m^2} = -0.25(/0.0) \frac{kN}{m^2}$

When you calculate the wind loads the first time ever, it might be very confusing in which direction you have to apply the loads. So let’s apply the wind loads with the c_pe.10 coefficient (for 10 m²) on our building.

Now we also have to do the same for the case that wind comes from the side.

Wind from Side

In the scenario that wind comes from the side, we have to define the area widths again. We have to redefine the geometry parameters.

Width of building	b	9.0 m
Length of building	d	13.0m
Height of building	h	6.0m

From those dimensions we can define e which determines the widths and depths of Areas F, G, H and I according to EN 1991-1-4:2005 Figure 7.8.

$$e = min(b, 2h)$$

$$e = min(9.0m, 2 \cdot 6.0m=12.0m) = 9.0m$$

From e we get the dimensions of the areas according to EN 1991-1-4:2005 Figure 7.8.

Area	Width	Depth
F	e/4 = 2.25m	e/10 = 0.9m
G	b-e/2 = 4.5m	e/10 = 0.9m
H	b = 9.0m	e/2 – e/10 = 3.6m
I	b = 9.0m	d-e/2 = 8.5m

As we all know, a picture tells more than a thousand words – so let’s visualize all of those numbers.

The external pressure coefficients for duo pitched roofs with the wind direction of $\Theta$ = 90° and a roof slope angle of 29° $\approx$ 30° can be taken from EN 1991-1-4:2005 Table 7.4b

Area	cpe.10	cpe.1
Area F	-1.1	-1.5
Area G	-1.4	-2.0
Area H	-0.8	-1.2
Area I	-0.5	-0.5

Based on our coefficients, we can now calculate the Wind pressure on external surfaces.

Area	we.10	we.1
Area F	$-1.1 \cdot 0.5 \frac{kN}{m^2} = -0.55 \frac{kN}{m^2} $	$-1.5 \cdot 0.5 \frac{kN}{m^2} = -0.75 \frac{kN}{m^2}$
Area G	$-1.4 \cdot 0.5 \frac{kN}{m^2} = -0.7 \frac{kN}{m^2} $	$-2.0 \cdot 0.5 \frac{kN}{m^2} = -1.0 \frac{kN}{m^2}$
Area H	$-0.8 \cdot 0.5 \frac{kN}{m^2} = -0.4 \frac{kN}{m^2} $	$-1.2 \cdot 0.5 \frac{kN}{m^2} = -0.6 \frac{kN}{m^2}$
Area I	$-0.5 \cdot 0.5 \frac{kN}{m^2} = -0.25 \frac{kN}{m^2} $	$-0.5 \cdot 0.5 \frac{kN}{m^2} = -0.25 \frac{kN}{m^2}$

Those wind area loads we can now visualize.

Conclusion

For a building of 6.0 m height, located in Copenhagen, Denmark, the wind load of a pitched roof is calculated for 2 directions and for 5 different wind areas as we learned in this article.

If you want to learn how to calculate the wind load on walls and pitched roofs, then check out the articles:

• Wind load calculation on flat roofs
• Calculation of the peak velocity pressure
• Wind load calculation on walls