Windlast Berechnung auf Wände {Tutorial 2025}
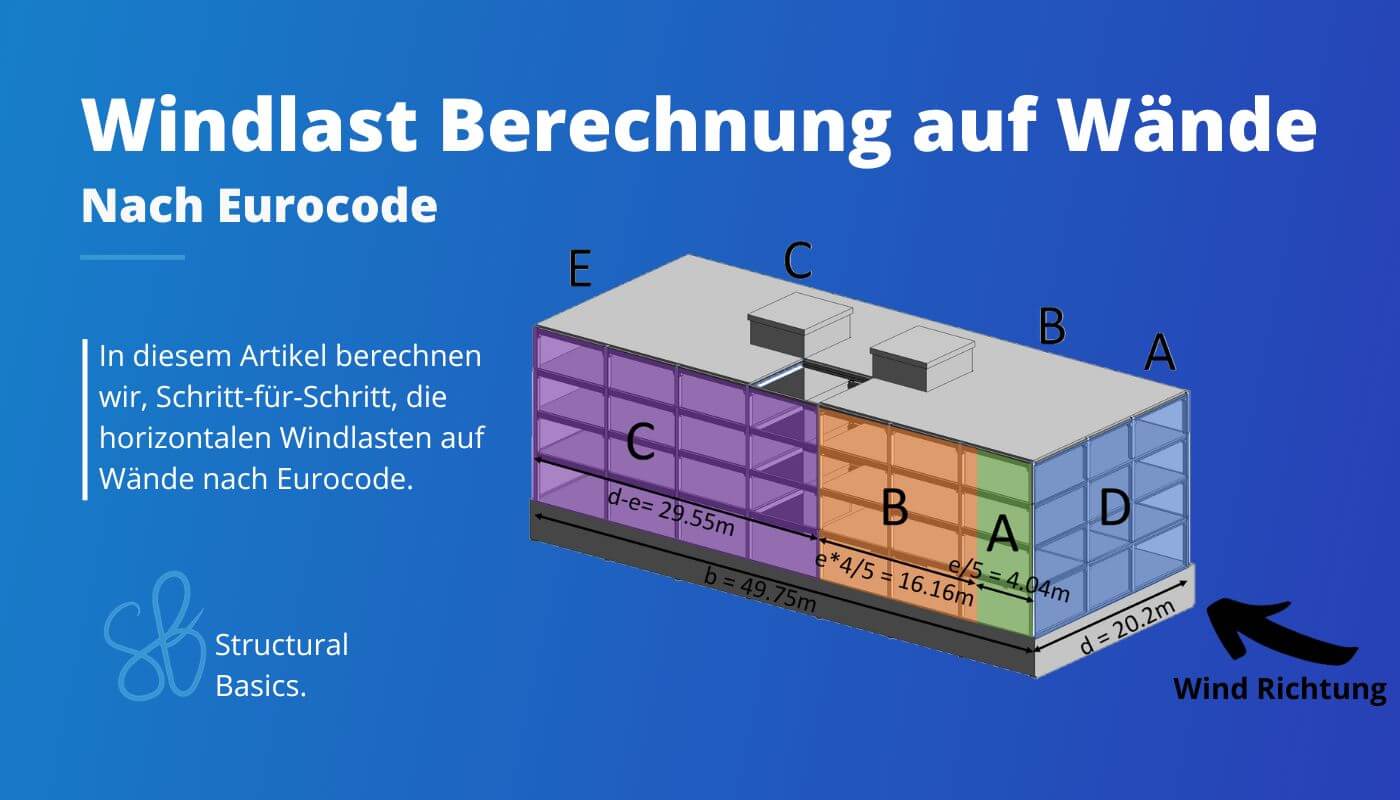
Die Windlasten auf Wände müssen in jeder Statik berücksichtigt werden, weil sie die Stabilität des Bauwerks beeinflussen. 💨🌬️
In diesem Blogpost zeigen wir, Schritt-für-Schritt, wie Du die Windlasten auf Wände nach Eurocode berechnest. 🧮🔢
Wir erklären Statik gerne anhand von Beispielen. 🖼️🖼️
Diesmal berechnen wir die horizontalen Windkräfte auf die Fassadenelemente des untenstehenden Bürogebäudes aus Betonfertigteilen.

Lasst uns starten. 🚀🚀
Windlast auf Wände – Berechnungsschritte
- Berechnung des Basisgeschwindigkeitsdrucks qp
- Definition der Geometrie des Gebäudes
- Berechnung der Abmessungen der Windzonen
- Ermittlung der the external pressure coefficients
- Calculate the wind pressures/loads
Definition der Geometrie und Parameter des Basisgeschwindigkeitsdrucks
Kurze Zusammenfassung der Werte, die wir berechnet haben, um den Basisgeschwindigkeitsdruck zu erhalten.
| Grundwert der Basisgeschwindigkeit | vb.0 | 22.5 m/s |
| Topographiebeiwert | c0 | 1.0 |
| Turbulenzfaktor | kl | 1.0 |
| Luftdichte | $\rho$ | 1.25 kg/m3 |
| Referenzhöhe von Geländekategorie II | z0.II | 0.05 m |
| Rauhigkeitslänge (Geländekategorie III) | z0 | 0.3 m |
| Geländefaktor | kr | 0.215 |
| Turbulenzintensität | Iv | 0.247 |
| Rauhigkeitsbeiwert | cr | 0.871 |
| Mittlere Windgeschwindigkeit | vm | 19.6 m/s |
| Basisgeschwindigkeitsdruck | qp | 0.66 kN/m2 |
Winddruck auf Oberflächen
Im Allgemeinen unterscheidet Eurocode zwischen Winddruck auf äußere und innere Flächen. Dieser Artikel konzentriert sich auf den Winddruck auf Außenflächen (Außenwinddruck).
Außenwinddruck we
Der Außenwindddruck wird mit folgender Formel (EN 1991-1-4 (5.1)) berechnet:
$$w_{e} = q_{p} \cdot c_{pe}$$
Mit
| qp | dem Basisgeschwindigkeitsdrucks |
| cpe | dem aerodynamische Beiwert für den Außendruck |
Der Beiwert cpe hat 2 verschiedene Werte. Dies is abhängig davon wie groß die Windbelastete Fläche ist.
Es gibt einen Wert für eine Fläche von 1 m2 und 10 m2. Diese beiden Werte werden in Eurocode folgendermaßen erklärt. 👇👇
| cpe.1 | Außendruckbeiwert für eine Fläche von 1 m2 and |
| cpe.10 | Außendruckbeiwert für eine Fläche von 10 m2 |
Du frägst dich jetzt wahrscheinlich: „Wann berechnet man schon mal ein tragendes Element, bei dem nur 1 m2 belastet wird?🤔🤔“
Das ist eine berechtigte Frage, denn das ist bei Trägern, Wänden und Decken fast nie der Fall. Aber für kleinere Elemente wie Verkleidungselemente der Fassade oder Befestigungen kommt cpe.1 ins Spiel (EN 1991-1-4 7.2.1 Anmerkung 1).
Als kurze Zusammenfassung:
cpe.10 wird üblicherweise für die Tragkonstruktion verwendet
cpe.1 wird für kleine Elemente innerhalb von Elementen verwendet, z.B. für Verkleidungen.
Genug Erklärung. Schauen wir uns jetzt die Werte der Beiwerte an. 🔎🔎
EN 1991-1-4 Tabelle 7.1 gibt Empfehlungen für cpe.10 und cpe.1. Dies bedeutet, dass diese Werte anderst im nationalen Anhang definiert sein können. Dies solltest du auf jeden Fall machen!
Tabelle 7.1 enthält Werte für 5 verschiedene Flächen A, B, C, D und E unseres Gebäudes.
Diese Flächen hängen davon ab, woher der Wind kommt, und können in EN 1991-1-4 Tabelle 7.1 gesehen werden. Für unser Bürogebäude können wir die Bereiche wie folgt definieren
Wind in Querrichtung
| Breite des Gebäudes | b | 49.75 m |
| Länge | d | 20.2 m |
| Höhe | h | 17.1m |
Aus diesen Abmessungen können wir e definieren, das die Breite der Flächen A und B gemäß EN 1991-1-4 Abbildung 7.5 bestimmt. 👇👇
$$e = min(b, 2h)$$
$$e = min(49,75m, 2*17,1m=34,4m) = 34,4m$$
Für den Fall e > d, der für uns zutrifft, ist die Breite der Fläche A definiert als
$$e/5 = 6.9m$$
Es wird verständlicher, wenn wir es in einem Bild visualiseren. 🖼️📷
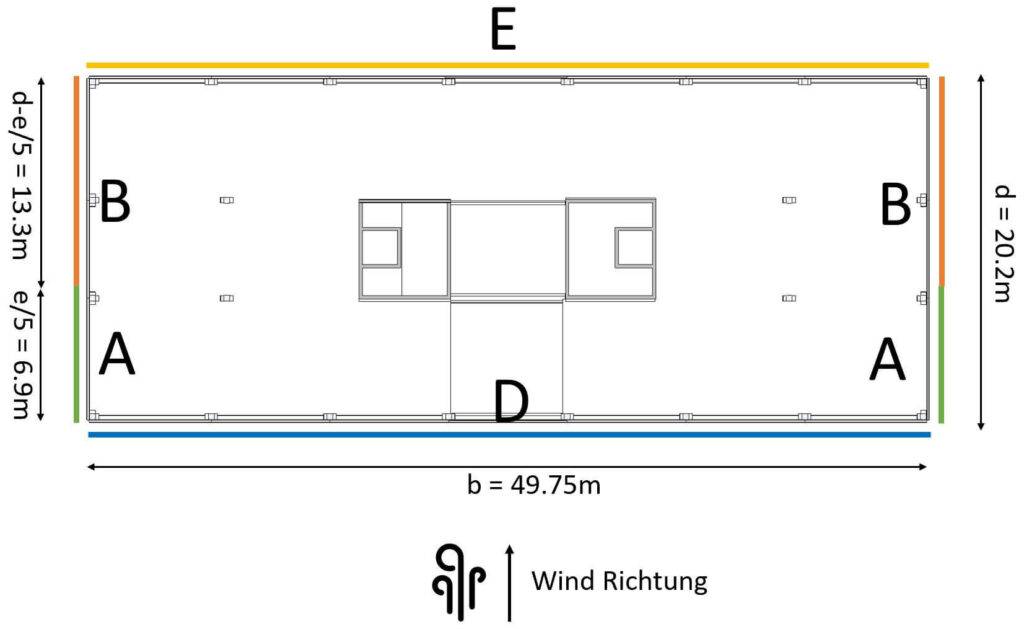
Die Wände auf dem Dach haben wir im folgenden Bild nicht hinzugefügt, damit es übersichtlicher aussieht. In den Berechnungen müssten wir diese Windflächen natürlich auch berücksichtigen.
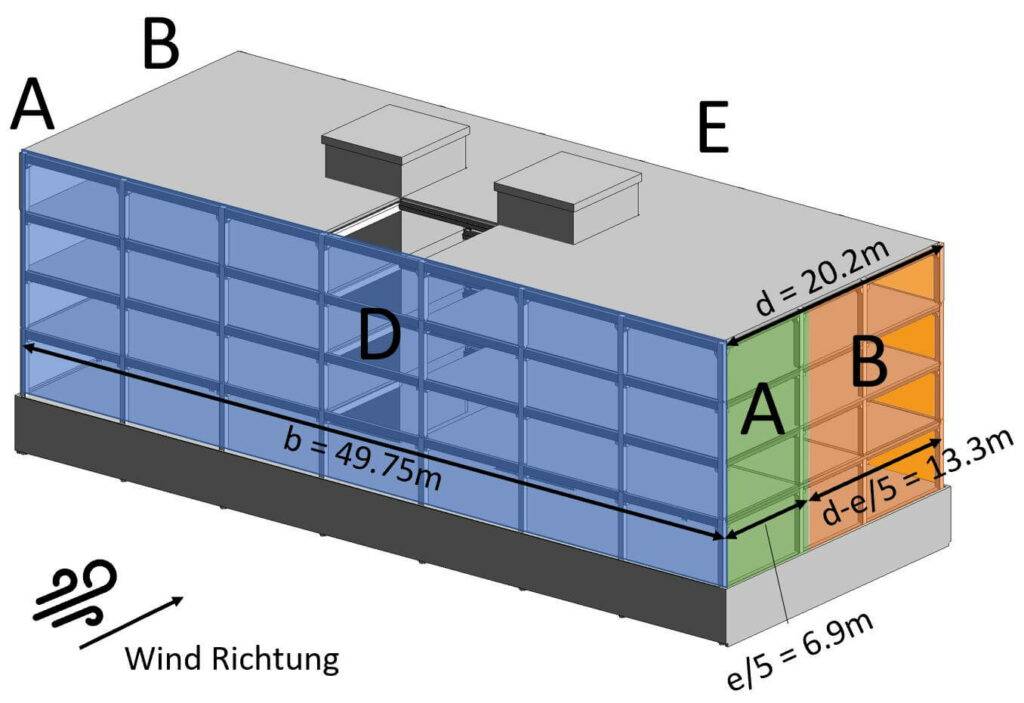
💡
Die Windflächen sind nicht an den untersten Wänden angebraucht, weil dies die Kellerwände sind, die nicht dem Wind ausgesetzt sind.
Als nächstes, leiten wir die Werte für den Winddruck für Außenflächen von der oben stehenden Formel ab. Den Basisgeschwindigkeitsdruck haben wir in diesem Artikel wie folgt berechnet:
$$q_{p} = 0.66 \frac{kN}{m^2}$$
Die Außendruckbeiwerte für rechteckige Gebäude können der EN 1991-1-4:2005 Tabelle 7.1 entnommen werden.
Für ein Verhältnis von Höhe zu Breite h/d = 17,1m/20,2m = 0,85, das < 1 und > 0,25 ist, ergeben sich die folgenden Werte. ⬇️⬇️
| Fläche | cpe.10 | cpe.1 |
| A | -1.2 | -1.4 |
| B | -0.8 | -1.1 |
| D | 0.8 | 1.0 |
| E | -0.5 | -0.5 |
Mit diesen Beiwerten können wir nun den Winddruck auf die Außenflächen berechnen.
| Fläche | we.10 | we.1 |
| A | $-1.2 \cdot 0.66 \frac{kN}{m^2} = -0.79 \frac{kN}{m^2} $ | $-1.4 \cdot 0.66 \frac{kN}{m^2} = -0.92 \frac{kN}{m^2}$ |
| B | $-0.8 \cdot 0.66 \frac{kN}{m^2} = -0.52 \frac{kN}{m^2} $ | $-1.1 \cdot 0.66 \frac{kN}{m^2} = -0.72 \frac{kN}{m^2}$ |
| D | $0.8 \cdot 0.66 \frac{kN}{m^2} = 0.52 \frac{kN}{m^2} $ | $1.0 \cdot 0.66 \frac{kN}{m^2} = 0.66 \frac{kN}{m^2}$ |
| E | $-0.5 \cdot 0.66 \frac{kN}{m^2} = -0.33 \frac{kN}{m^2} $ | $-1.1 \cdot 0.66\frac{kN}{m^2} = -0.33 \frac{kN}{m^2}$ |
Wenn man die Windlasten zum ersten Mal berechnet, kann es sehr verwirrend sein, in welche Richtung man die Lasten aufbringen muss.
Also lasst es uns gemeinsam, für die Windlasten (10 m2), machen.
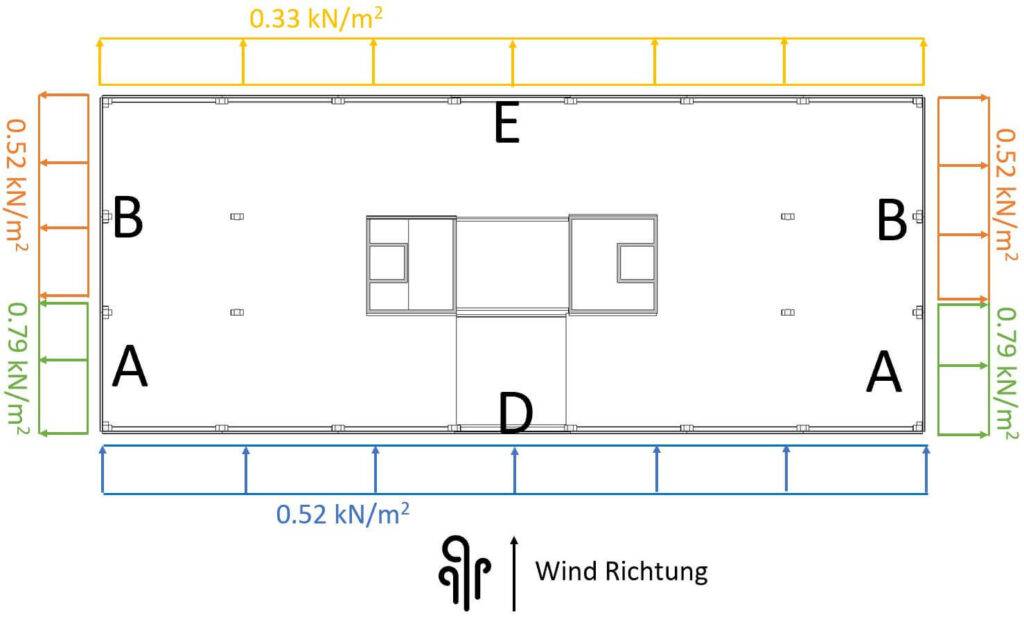
Zum besseren Verständnis visualisieren wir das auch in 3D.
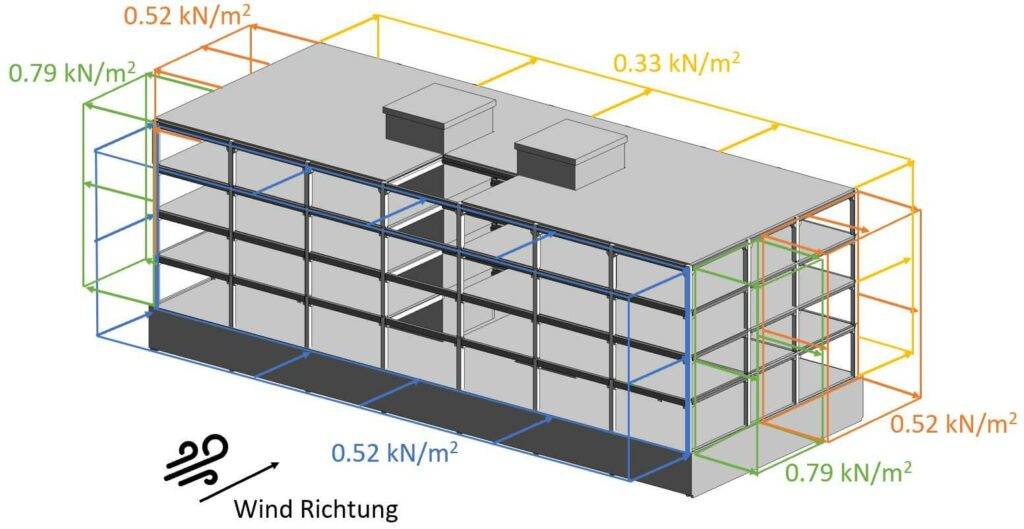
Nun machen wir das Gleiche, für die Situation, dass der Wind von der Seite weht.
Wind in Längsrichtung
Für das Szenario, dass der Wind von der Seite (Längsrichtung) kommt, müssen wir die Flächenbreiten neu berechnen. Dafür definieren wir zuerst die Geometrieparameter neu.
| Breite des Gebäudes | b | 20.2 m |
| Länge des Gebäudes | d | 49.75 m |
| Höhe des Gebäudes | h | 17.1m |
Aus diesen Abmessungen lässt sich e gemäß EN 1991-1-4 Abbildung 7.5 definieren
$$e = min(b, 2h)$$
$$e = min(20.2m, 2 \cdot 17.1m=34.4m) = 20.2m$$
Für den Fall e < d, der für uns zutrifft, ist die Breite der Fläche A definiert als:
$$e/5 = 4.04m$$
Der Bereich B wird berechnet als
$$e \cdot 4/5 = 16.16m$$
Der Bereich C ist also der Rest von d und wird berechnet als
$$d – e = 49.75m – 20.2m = 29.55m$$
Veranschaulichen wir alle diese Zahlen in 2D und 3D. 🖼️👇
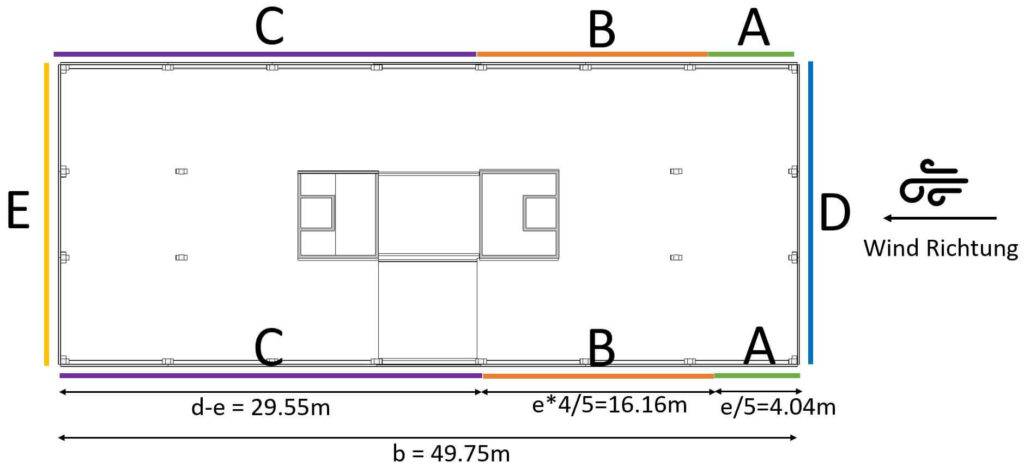
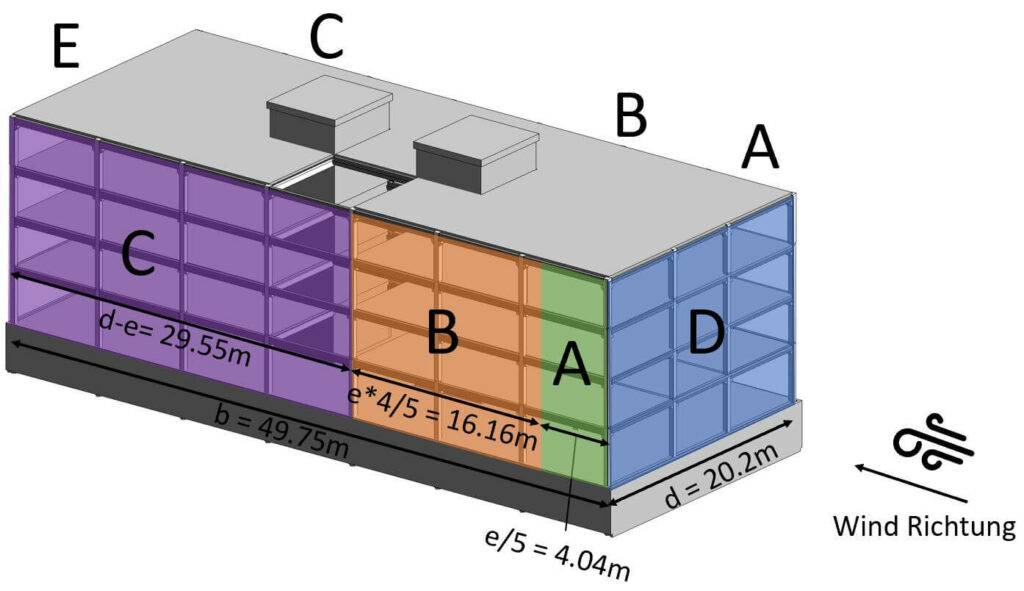
Für ein Verhältnis von Höhe zu Breite h/d = 17,1m/49,75m = 0,34, was < 1 und > 0,25 ist, erhalten wir die folgenden Beiwerte, die in der untenstehenden Tabelle aufgeführt sind. Man sieht, dass wir die gleichen Beiwerte für A, B, D und E wie für Wind in Querrichtung erhalten, aber zusätzlich erhalten wir jetzt einen Wert für C (EN 1991-1-4:2005 Tabelle 7.1).
| Fläche | cpe.10 | cpe.1 |
| Area A | -1.2 | -1.4 |
| Area B | -0.8 | -1.1 |
| Area C | -0.5 | -0.5 |
| Area D | 0.8 | 1.0 |
| Area E | -0.5 | -0.5 |
Mit diesen Beiwerten können wir nun den Winddruck auf Außenflächen in Längsrichtung berechnen.
| Area | we.10 | we.1 |
| A | $-1.2 \cdot 0.66 \frac{kN}{m^2} = -0.79 \frac{kN}{m^2} $ | $-1.4 \cdot 0.66 \frac{kN}{m^2} = -0.92 \frac{kN}{m^2}$ |
| B | $-0.8 \cdot 0.66 \frac{kN}{m^2} = -0.52 \frac{kN}{m^2} $ | $-1.1 \cdot 0.66 \frac{kN}{m^2} = -0.72 \frac{kN}{m^2}$ |
| C | $-0.5 \cdot 0.66 \frac{kN}{m^2} = -0.33 \frac{kN}{m^2} $ | $-0.5 \cdot 0.66 \frac{kN}{m^2} = -0.33 \frac{kN}{m^2}$ |
| D | $0.8 \cdot 0.66 \frac{kN}{m^2} = 0.52 \frac{kN}{m^2} $ | $1.0 \cdot 0.66 \frac{kN}{m^2} = 0.66 \frac{kN}{m^2}$ |
| E | $-0.5 \cdot 0.66 \frac{kN}{m^2} = -0.33 \frac{kN}{m^2} $ | $-1.1 \cdot 0.66 \frac{kN}{m^2} = -0.33 \frac{kN}{m^2}$ |
Diese Windflächenlasten können wir nun in einem Grundriss visualisieren. 📷📷
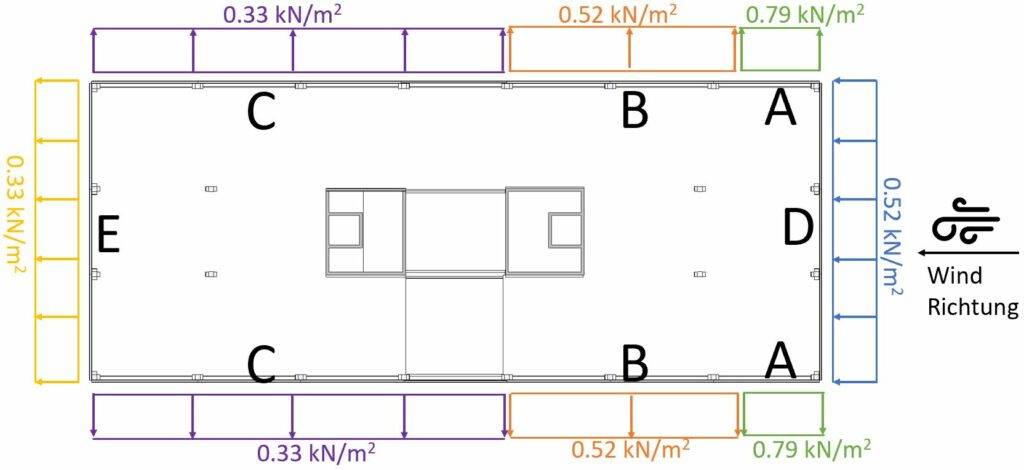
Abminderung der Windlast der Flächen D und E
Nach EN 1991-1-4 7.2.2 (3) können die Windlasten der Flächen D und E reduziert werden, wenn sie folgende Kriterien erfüllen: 👇👇
$$h/d <1 $$
Wind in Querrichtung
$$h/d = 17.1m/20.2m = 0.85 < 1$$
The criteria are met, and the forces in Areas D and E can be reduced by the factor 0.85.
Das Kriterium ist erfüllt, und die Windlasten auf die Flächen D und E können um den Faktor 0,85 reduziert werden.
| Fläche | we.10 | we.1 |
| D | $0.85 \cdot 0.52 \frac{kN}{m^2} = 0.44 \frac{kN}{m^2} $ | $0.85 \cdot 0.66 \frac{kN}{m^2} = 0.56 \frac{kN}{m^2}$ |
| E | $0.85 \cdot (-0.33 \frac{kN}{m^2}) = -0.28 \frac{kN}{m^2} $ | $0.85 \cdot (-0.33 \frac{kN}{m^2}) = -0.28 \frac{kN}{m^2}$ |
Wind in Längsrichtung
$$h/d = 17.1m/49.75m = 0.34 < 1$$
Das Kriterium ist erfüllt, und die Windlasten auf die Flächen D und E können um den Faktor 0,85 reduziert werden.
| Fläche | we.10 | we.1 |
| D | $0.85 \cdot 0.52 \frac{kN}{m^2} = 0.44 \frac{kN}{m^2} $ | $0.85 \cdot 0.66 \frac{kN}{m^2} = 0.56 \frac{kN}{m^2}$ |
| E | $0.85 \cdot (-0.33 \frac{kN}{m^2}) = -0.28 \frac{kN}{m^2} $ | $0.85 \cdot (-0.33 \frac{kN}{m^2}) = -0.28 \frac{kN}{m^2}$ |
Fazit
Zusammenfassend, kann man sagen, dass man die Windlasten auf Gebäude immer für 2 Richtungen berechnen muss. Die Windlasten haben verschieden Werte für die verschiedenen Flächen A, B, C, D und E, die mit den Winddruckbeiwerten und dem Basisgeschwindigkeitsdruck berechnen.
Zusätzlich muss die Windlast auch für das Dach berechnet werden. Wir haben dies in den folgenden Artikeln detailiert aufgezeigt:
Windlasten auf Wände FAQ
Die Windlasten auf Wände werden mit Formeln aus dem Eurocode EN1991-1-4 berechnet.
Windlasten sind wichtig, weil sie die Stabilität von Gebäuden und Tragwerken beeinflussen. Zu hohe Windlasten können zu statischen Schäden, wie z.B. Rissen in Betonwände, bis hin zum Kollaps eines Bauwerks führen.
![Die 5 Lasten Auf Dächern [Überblick]](https://www.structuralbasics.com/wp-content/uploads/2023/09/Dachlasten-Statik-768x439.jpg)

![Schneelast Berechnung eines Flachdachs [2025]](https://www.structuralbasics.com/wp-content/uploads/2023/12/Schneelast-eines-Flachdachs-768x439.jpg)
