Widerstandsmoment Formeln Verschiedener Querschnitte {2024}

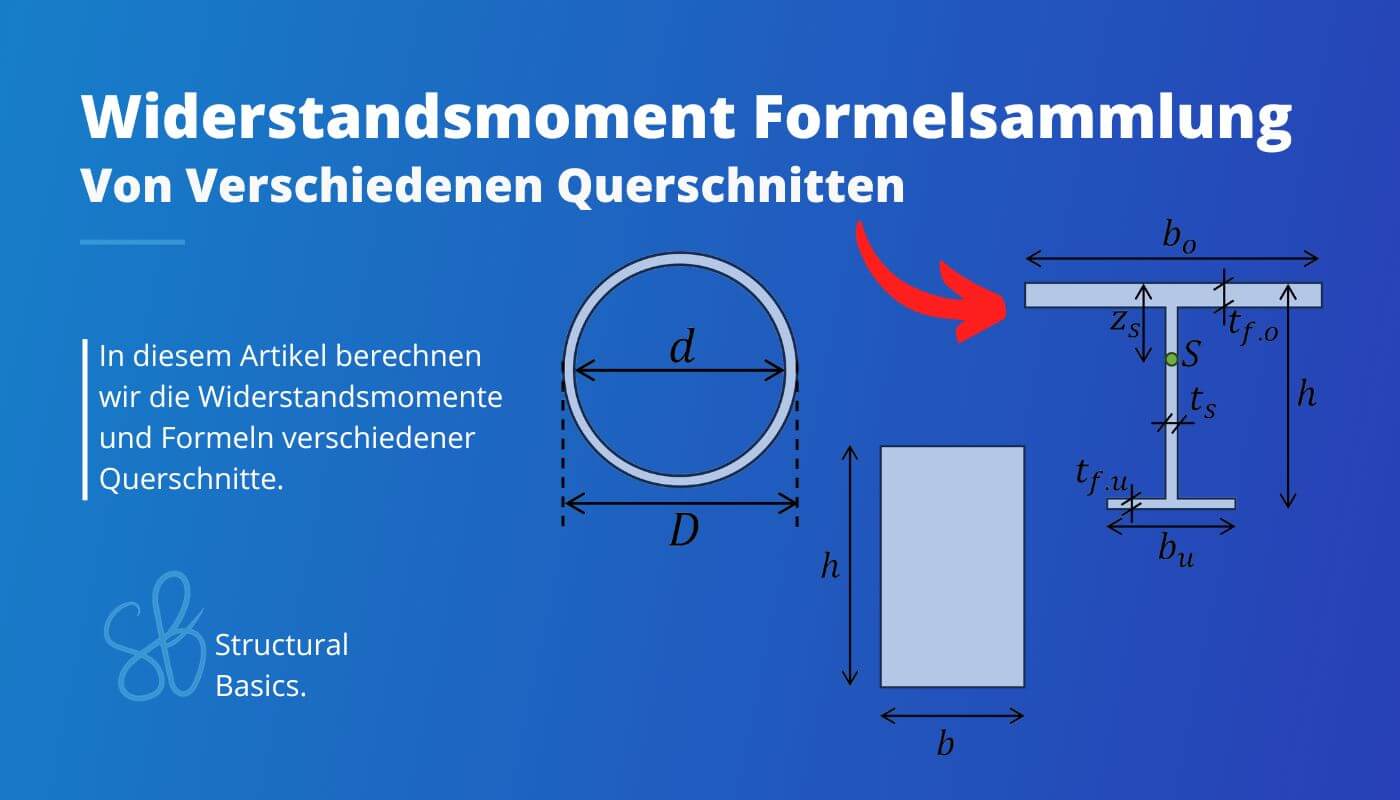
Das Widerstandsmoment ist eine Eigenschaft eines Objekts, die angibt, wie gut ein Material sich gegen Biegung oder Verformung unter äußerer Belastung widerstehen kann.

Wenn ein Objekt eine andere Form hat, hat es auch ein anderes Widerstandsmoment. In diesem Blogpost findest du Widerstandsmoment Formeln für verschiedene Formen, um es schnell berechnen zu können.

Lass uns starten, die Widerstandsmomente zu berechnen. 🚀🚀

Widerstandsmoment Formel

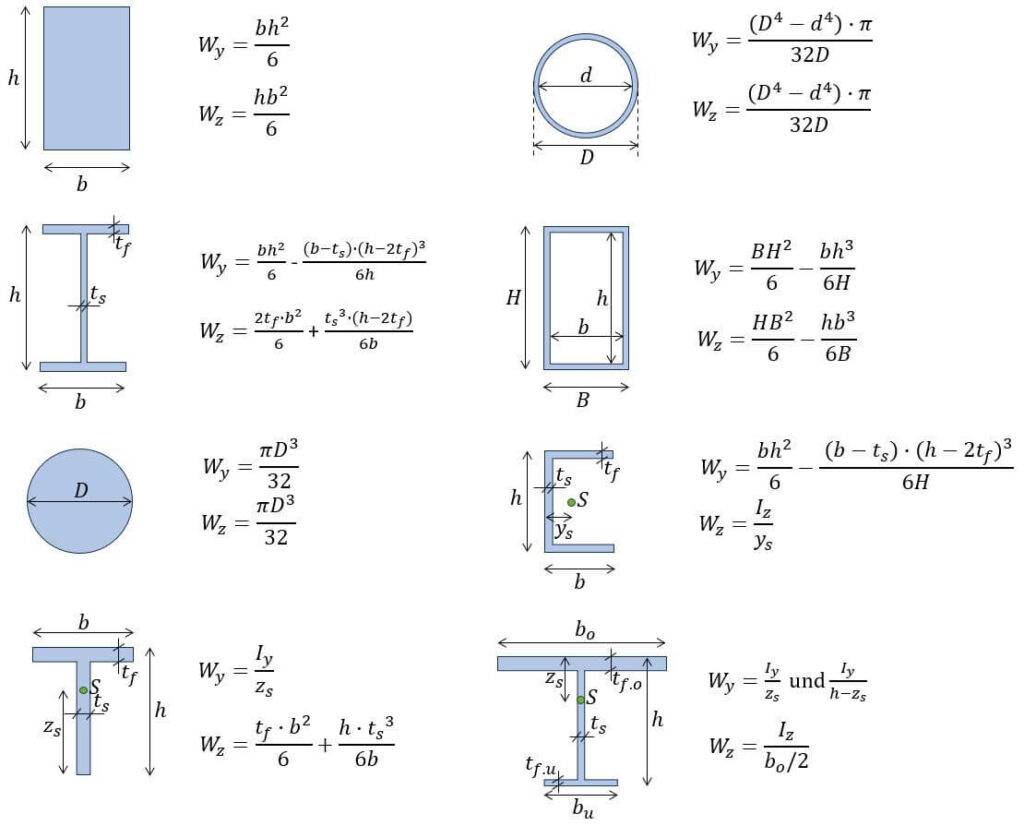
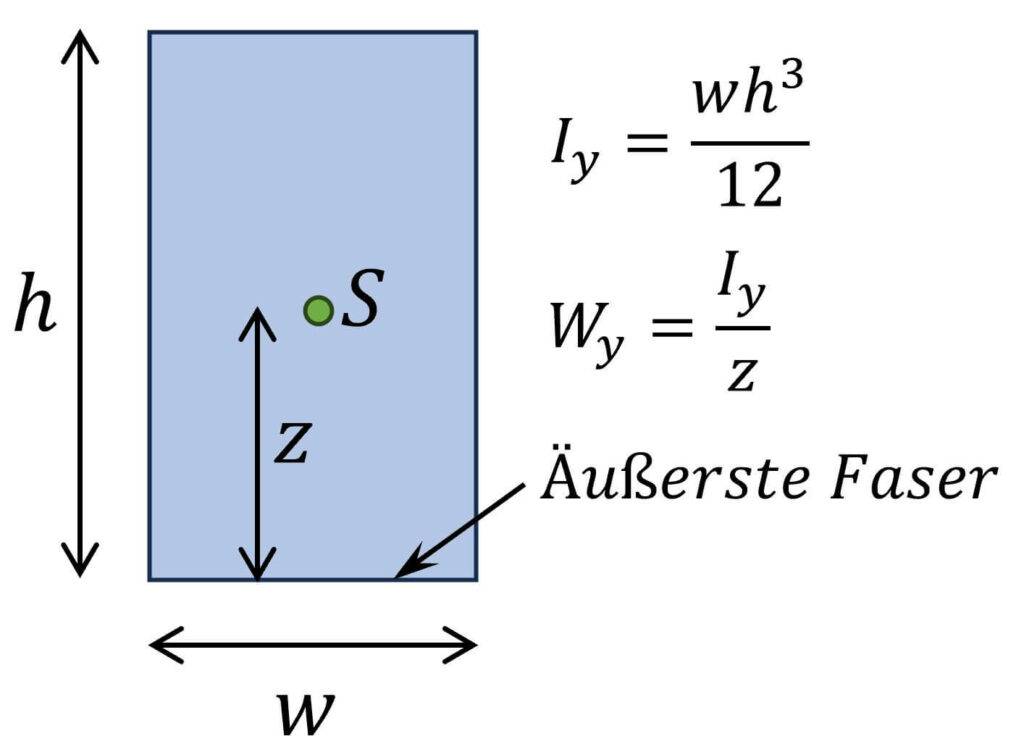
Um das Widerstandsmoment eines Querschnitts zu ermitteln, wird das Flächenträgheitsmoment I durch den Abstand vom Schwerpunkt z zur äußersten Faser geteilt.

$$W = \frac{I}{z}$$

Was Ist Das Widerstandsmoment?

Das Widerstandsmoment ist eine querschnittsbezogene geometrische Eigenschaft von statischen Elementen wie Trägern, Stützen, Platten usw. Es wird zur Berechnung von Spannungen in Querschnitten verwendet.

Im Allgemeinen kann gesagt werden, dass je größer die Abmessungen eines Querschnitts bei gegebener Belastung sind, desto größer ist der Widerstandsmoment und desto geringer ist die Biegespannung.

1. Rechteck/ Vollquerschnitt

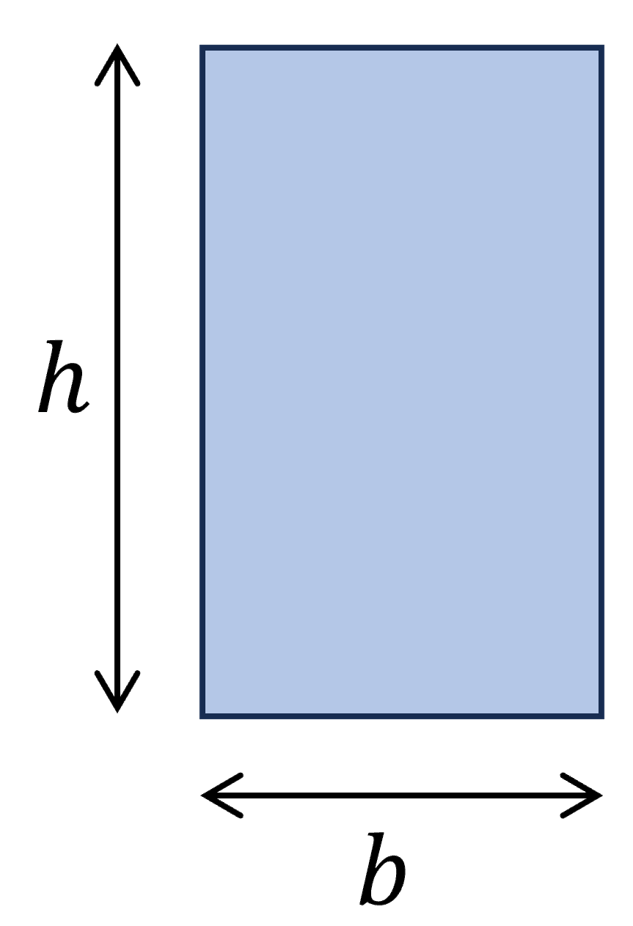
Beispiel Berechnung des Widerstandsmoment

h = 240 mm, b = 120 mm

Starke Achse:

$W_y = \frac{1}{6} \cdot h^2 \cdot b = \frac{1}{6} \cdot (240mm)^2 \cdot 120mm = 1.15 \cdot 10^6 mm^3$

Schwache Achse:

$W_z = \frac{1}{6} \cdot h \cdot b^3 = \frac{1}{6} \cdot 240mm \cdot (120mm)^2= 5.76 \cdot 10^5 mm^3$

Wo wird das Widerstandsmoment eines rechteckigen Querschnitts in echten Projekten angewendet?

• Biegenachweis eines Holzbalkens
• Biegenachweis von Stahlplatten
• Biegenachweis eines Stahlbeton Balken

2. I- und H Querschnitt

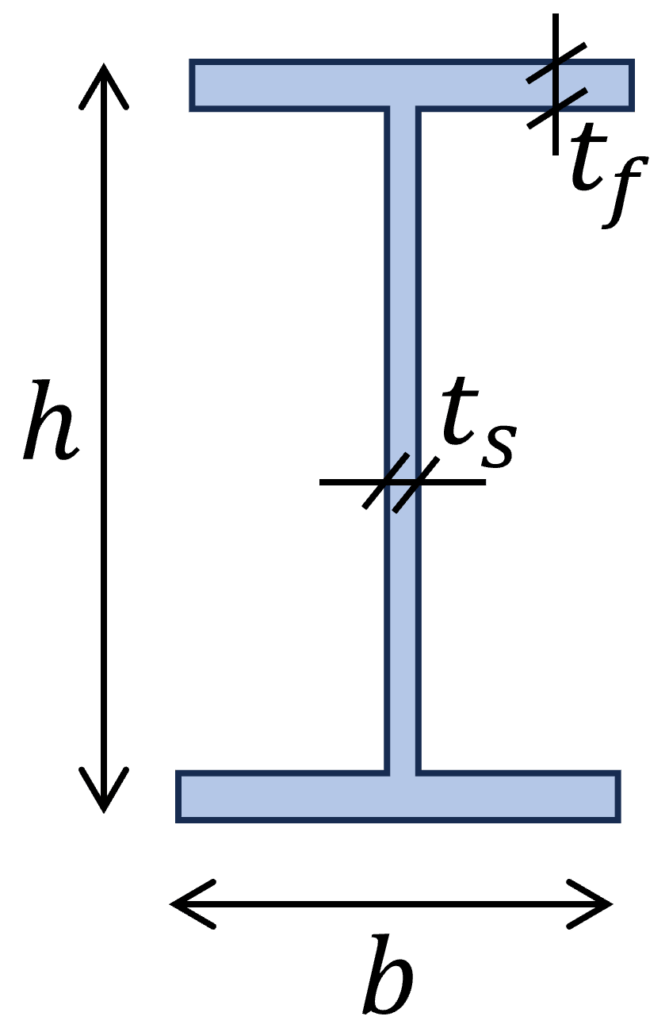
Beispiel Berechnung des Widerstandsmoment

$h$ = 300mm, $b$ = 150mm, $t_f$ = 10mm, $t_s$ = 7mm

Starke Achse:

$W_y = \frac{b \cdot h^2}{6} – \frac{(b-t_s) \cdot (h-2\cdot t_f)^3}{6h} = \frac{150mm \cdot (300mm)^2}{6} – \frac{(150mm-7mm) \cdot (300mm-2\cdot 10mm)^3}{6h} =  5.06 \cdot 10^5 mm^3$

Schwache Achse:

$W_z = \frac{b^2 \cdot 2t_f}{6} + \frac{t_s^3 \cdot (h-2t_f)}{6b} = \frac{(150mm)^2 \cdot 2 \cdot 10mm}{6} + \frac{(7mm)^3 \cdot (300mm-2 \cdot 10mm)}{6\cdot 150mm} = 7.51 \cdot 10^4 mm^3$

Wo wird das Widerstandsmoment eines I- bzw. H- Querschnitts in echten Projekten angewendet?

• Biegenachweis eines IPE Stahlträgers
• Stabilitätsnachweis einer HEB Stahlstütze

3. Kreis Querschnitt

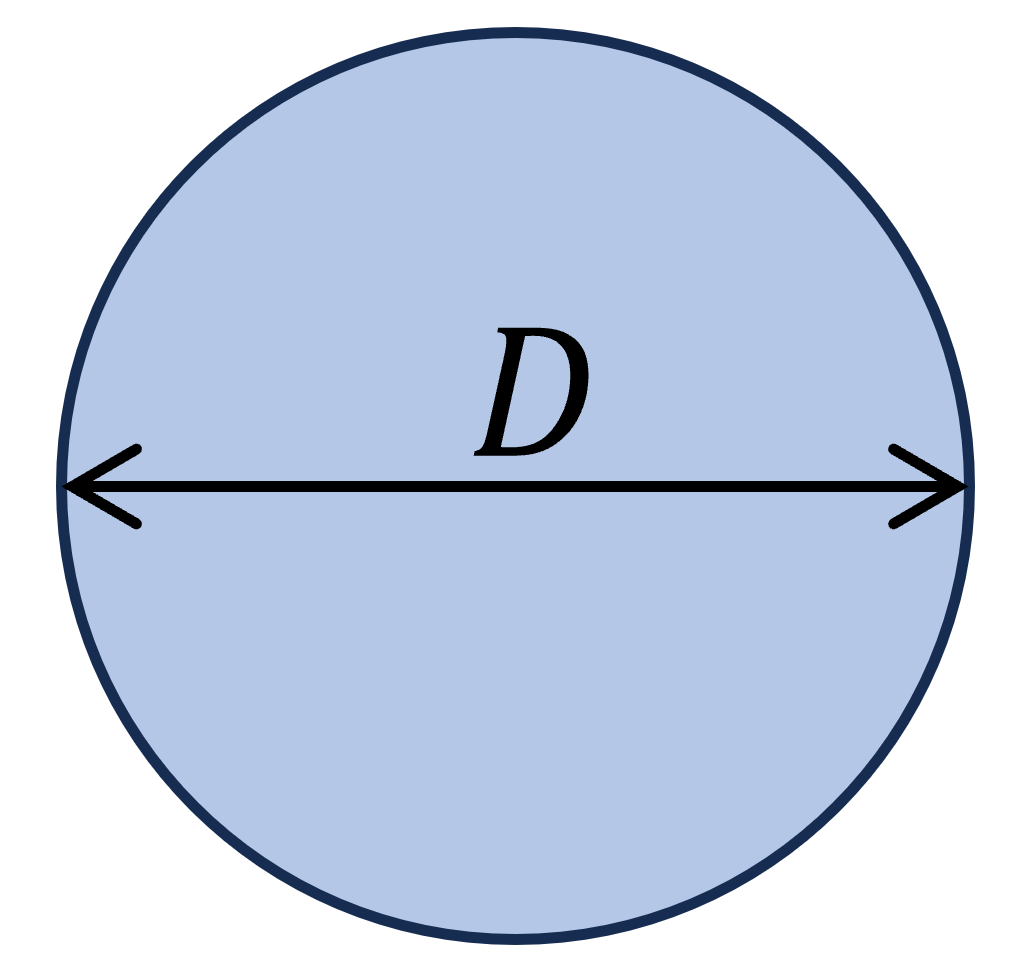
Beispiel Berechnung des Widerstandsmoment

D = 100mm

Starke Achse:

$W_y = \frac{D^3 \cdot \pi}{32} = \frac{(100mm)^3 \cdot \pi}{32} = 9.82 \cdot 10^4 mm^3$

Schwache Achse:

$W_z = \frac{D^3 \cdot \pi}{32} = \frac{(100mm)^3 \cdot \pi}{32} = 9.82 \cdot 10^4 mm^3$

Wo wird das Flächenträgheitsmoment eines Kreisquerschnitts in echten Projekten angewendet?

• Nachweis einer Stahlbeton Stütze

4. Kreisrohr Querschnitt

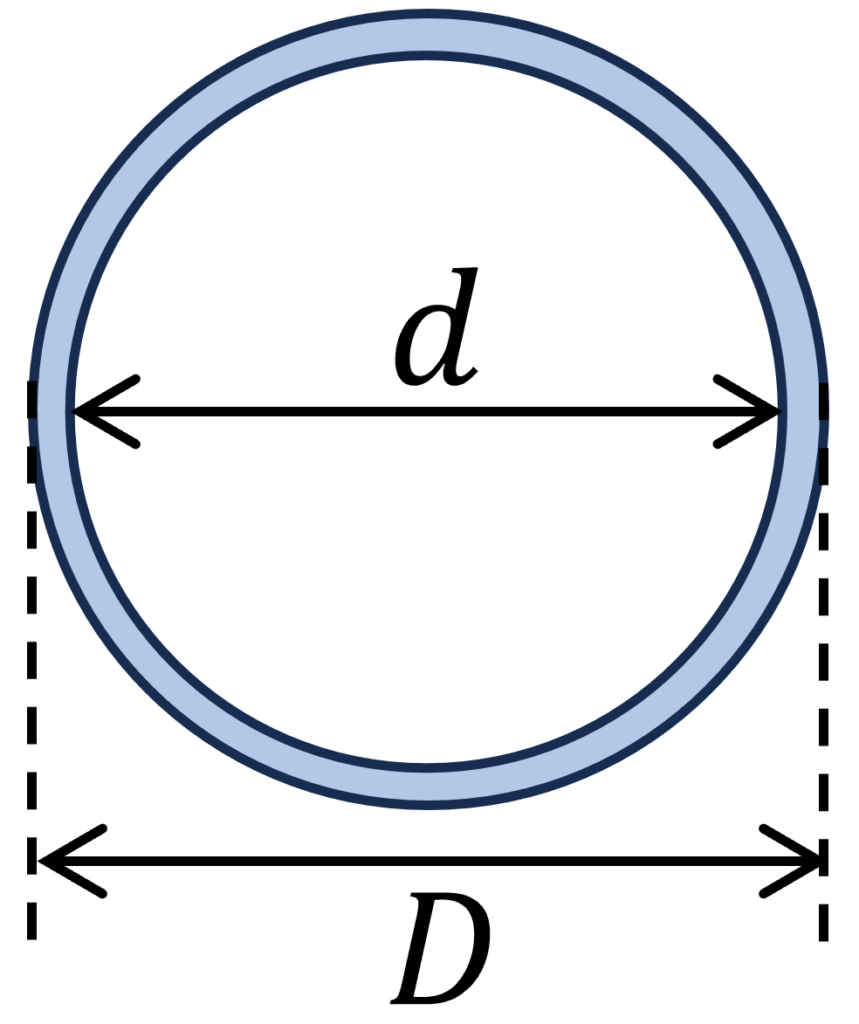
Beispiel Berechnung des Widerstandsmoment

D = 100mm, d = 90mm

Starke Achse:

$W_y = \frac{(D^4 – d^4) \cdot \pi}{32D} = \frac{((100mm)^4 – (90mm)^4) \cdot \pi}{32 \cdot 100mm} = 3.376 \cdot 10^4 mm^3$

Schwache Achse:

$W_z = \frac{(D^4 – d^4) \cdot \pi}{32D} = \frac{((100mm)^4 – (90mm)^4) \cdot \pi}{32 \cdot 100mm} = 3.376 \cdot 10^4 mm^3$

Wo wird das Widerstandsmoment eines Kreisrohr Querschnitts in echten Projekten angewendet?

• Biege und Stabilitätsnachweise einer Kreisrohrstütze

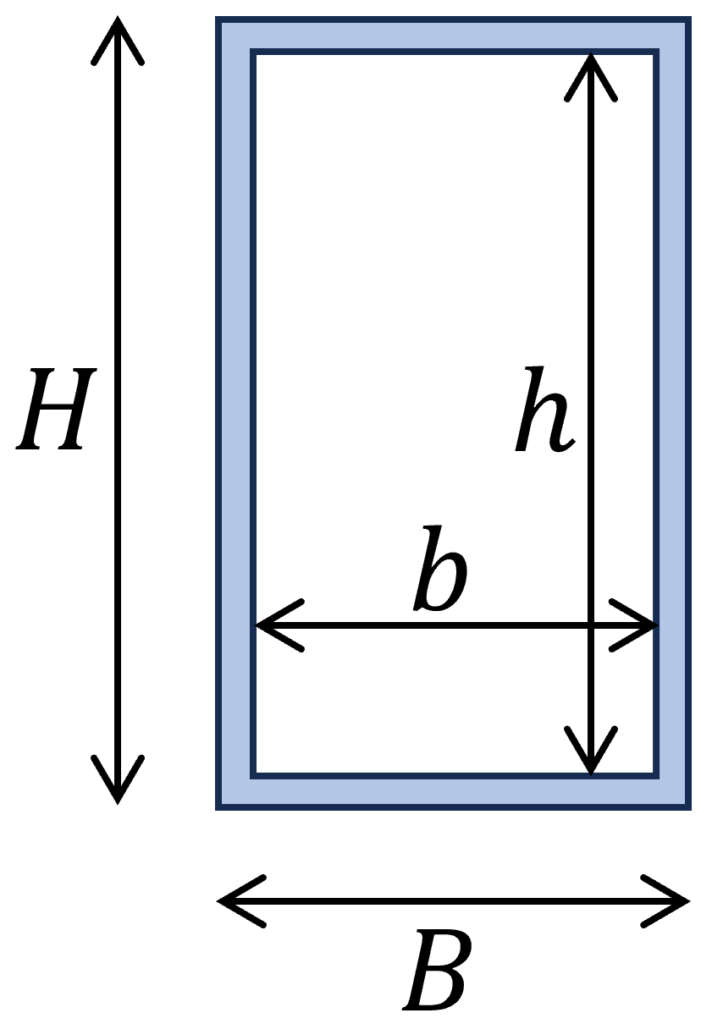
5. Rechteckiger Hohlquerschnitt

Beispiel Berechnung des Widerstandsmoment

B = 120mm, H = 240mm, b = 100mm, h = 220mm

Starke Achse:

$W_y = \frac{B \cdot H^2}{6} – \frac{b \cdot h^3}{6H} = \frac{120mm \cdot (240mm)^2}{6} – \frac{100mm \cdot (220mm)^3}{6\cdot 240mm} = 4.126 \cdot 10^5 mm^3$

Schwache Achse:

$W_z = \frac{B^2 \cdot H}{6} – \frac{b^3 \cdot h}{6B} = \frac{(120mm)^2 \cdot 240mm}{6} – \frac{(100mm)^3 \cdot 220mm}{6 \cdot 120mm} = 2.704 \cdot 10^5 mm^3$

Wo wird das Widerstandsmoment eines rechteckigen Hohlquerschnitts in echten Projekten angewendet?

• Biege und Stabilitätsnachweise einer Stahlstütze/ -balken (SHS und RHS Querschnitte)

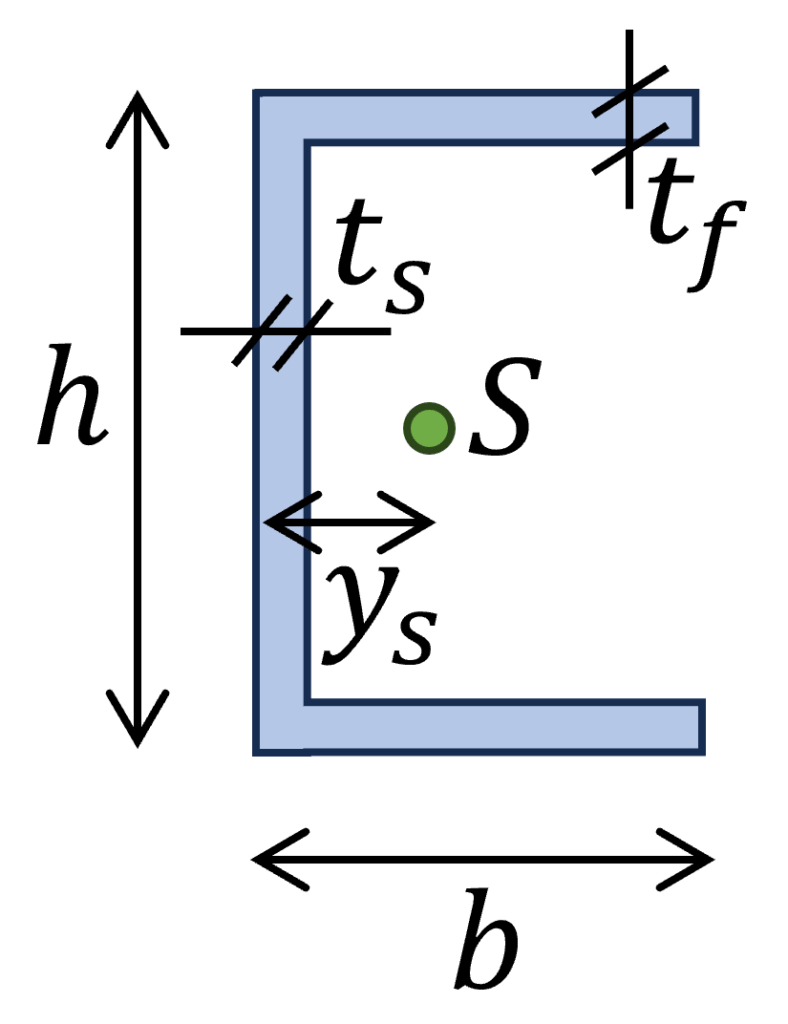
6. U/C Querschnitt

Beispiel Berechnung

b = 100mm, h = 80mm, $t_f$ = 5mm, $t_s$ = 5mm

Starke Achse:

$W_y = \frac{b \cdot h^2}{6} – \frac{(b – t_s) \cdot (h – 2t_f)^3}{6H} = \frac{100mm \cdot (80mm)^2}{6} – \frac{(100mm – 5mm) \cdot (80mm – 2 \cdot 5mm)^3}{6 \cdot 80mm} = 3.878 \cdot 10^4 mm^3$

Wo wird das Widerstandsmoment eines U Profils in echten Projekten angewendet?

• Biege und Stabilitätsnachweise eines C-Querschnitts, der Teil einer Decke oder Windverbund ist.

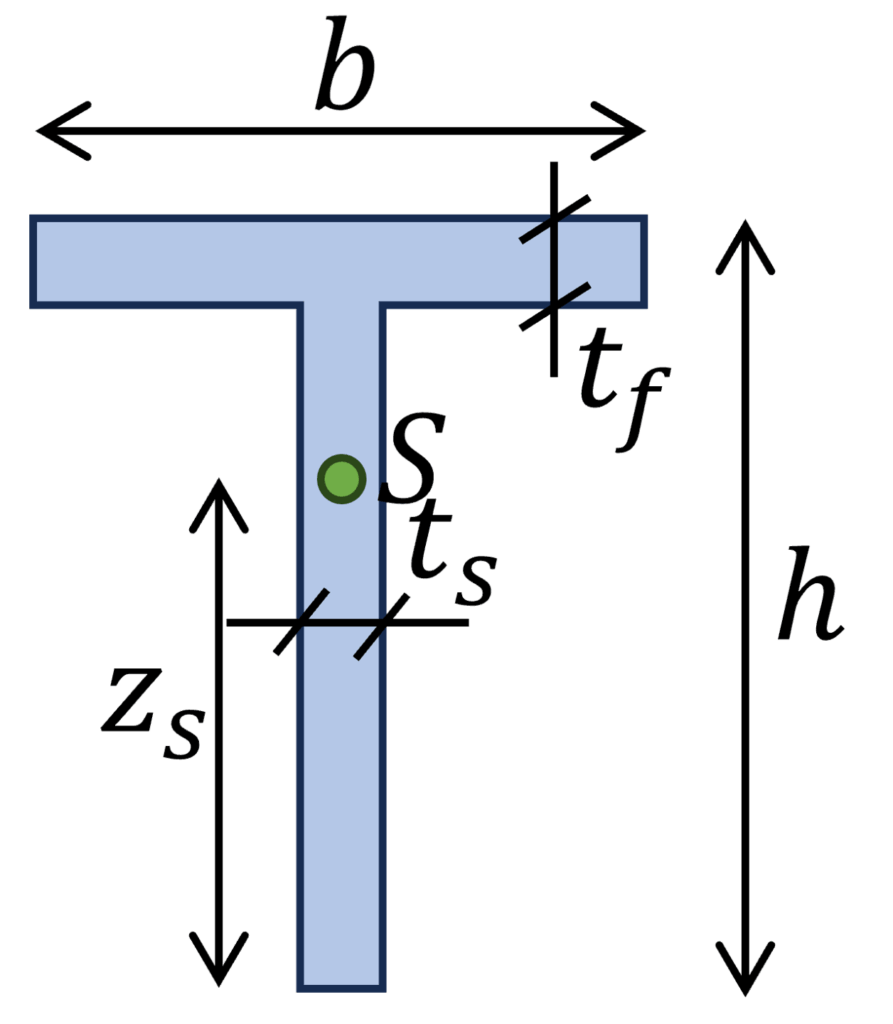
7. T Querschnitt

Beispiel Berechnung

b = 100mm, h = 100mm, $t_f$ = 5mm, $t_s$ = 5mm

Schwache Achse:

$W_z = \frac{t_f \cdot b^2}{6} + \frac{h \cdot t_s^3}{6 \cdot b}$
$W_z = \frac{5mm \cdot (100mm)^2}{6} + \frac{100mm \cdot (5mm)^3}{6 \cdot 100mm}$
$W_z = 8.354 \cdot 10^3 mm^3$

8. Unsymmetrischer I-Querschnitt

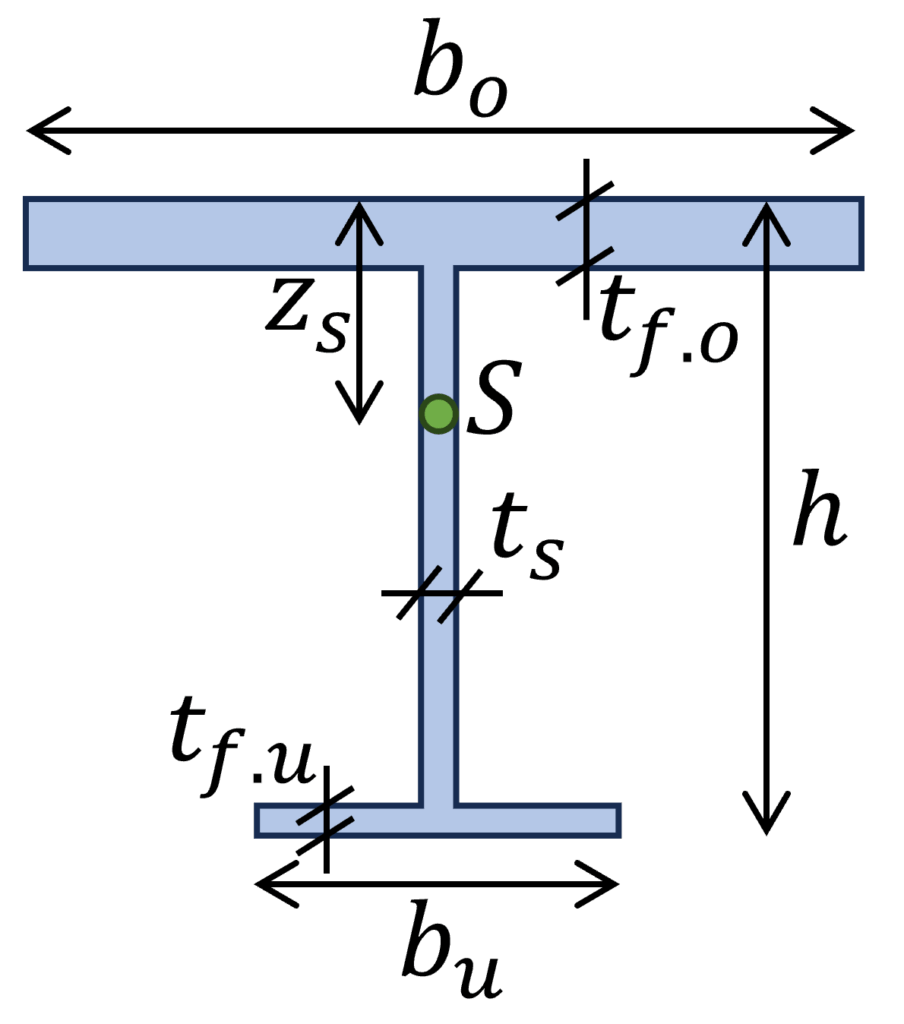
Abstand zum Schwerpunkt S:

$z_s = (\frac{1}{b_u \cdot t_{f.o}+b_u \cdot t_{f.u}+(h-t_{f.o}-t_{f.u}) \cdot t_s}) \cdot (b_o \cdot t_{f.o} \cdot \frac{t_{f.o}}{2}+(h-t_{f.o}-t_{f.u}) \cdot t_s \cdot(t_{f.o}+\frac{(h-t_{f.o}-t_{f.u}}{2})$
$+b_u \cdot t_{f.u} \cdot(h-\frac{t_{f.u}}{2}))$

Klicke hier, um die Formeln der Trägheitsmomente zu sehen.

Beispiel Berechnung

$b_o = 200mm$, $b_u = 100mm$, $h = 200mm$, $t_{f.o} = 20mm$, $t_{f.u} = 10mm$, $t_s = 10mm$

Schwache Achse:

$I_z = \frac{20mm \cdot (200mm)^3}{12} + \frac{(200mm-20mm-10mm)\cdot (10mm)^3}{12} +\frac{10mm \cdot (100mm)^3}{12} = 1.418 \cdot 10^7 mm^4$

$W_z = \frac{I_z}{b_o/2} = \frac{1.418 \cdot 10^7 mm^4}{100mm} = 1.418 \cdot 10^5 mm^3$

Abstand vom Schwerpunkt S:

$z_s = (\frac{1}{200mm \cdot 20mm+100mm \cdot 10mm+(200mm-20mm-10mm) \cdot 10mm}) \cdot$
$(200mm \cdot 20mm \cdot \frac{20mm}{2}+(200mm-20mm-10mm) \cdot 10mm \cdot(20mm+\frac{200mm-20mm-10mm}{2})$
$+100mm \cdot 10mm \cdot(200mm-\frac{10mm}{2})) = 61.72mm$

Starke Achse:

$I_y=\frac{200mm \cdot (20mm)^3}{12}+200mm \cdot 20mm \cdot(61.72mm-\frac{20mm}{2})^2+\frac{10mm \cdot(200mm-20mm-10mm)^3}{12}$
$+10mm \cdot(200mm-20mm-10mm) \cdot(61.72mm-(20mm+\frac{(200mm-20mm-10mm)}{2}))^2$
$+\frac{100mm \cdot (10mm)^3}{12}+100mm \cdot 10mm \cdot(61.72mm-200mm-\frac{10mm}{2})^2 = 3.865 \cdot 10^7 mm^4$

Untere Faser:

$W_y = \frac{I_y}{h – z_s} = \frac{3.865 \cdot 10^7 mm^4}{200mm – 61.7mm} = 2.795 \cdot 10^5 mm^3$

Fazit

Das Widerstandsmoment und das Flächenträgheitsmoment sind wichtige Parameter in der Statik und daher ist es sehr empfehlenswert zu wissen, wie man sie für verschiedene Querschnitte berechnet.

In den folgenden Blogposts zeigen wir Schritt-für-Schritt, wie man die beiden geometrischen Eigenschaften berechnet:

• Berechnung des Widerstandsmoment
• Flächenträgheitsmoment Berechnung eines I-Trägers
• Trägheitsmoment Berechnung {Schritt-für-Schritt}

Falls dich Statik interessiert, dann kännten dir folgende Posts weiterhelfen.

• Statik eines Pfettendachs
• Statische Berechnung eines Punktfundaments