Dachsparren berechnen {Schritt-für-Schritt Statik Anleitung}

In diesem Beitrag, zeigen wir was ein Sparrendach ist, wie es funktioniert und Du es nach Eurocode EN 1995-1-1 berechnest.

Lass uns starten. 🚀🚀

Was ist ein Sparrendach?

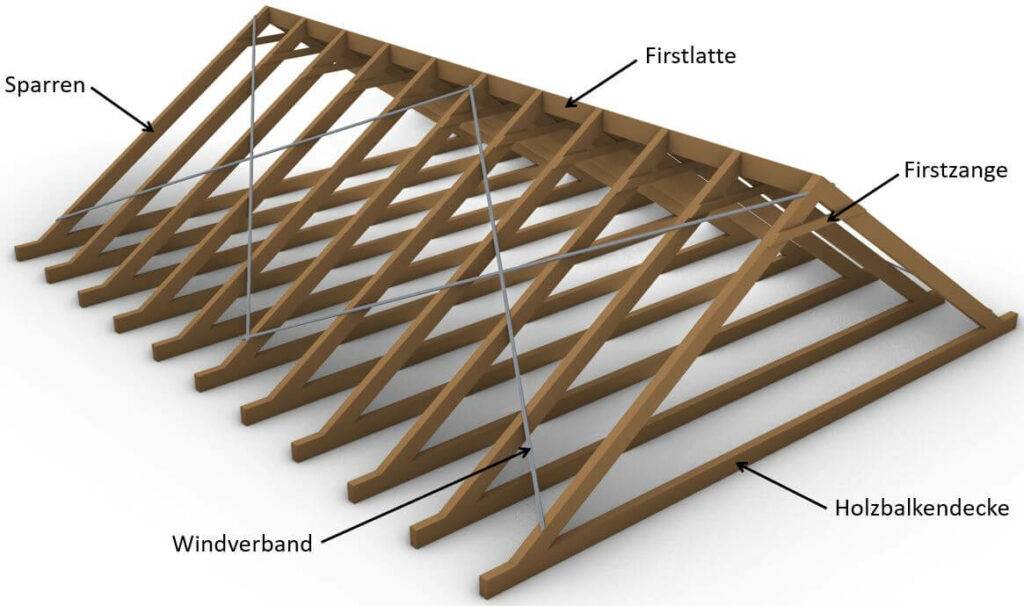
Das Sparrendach besteht aus 2 Sparren, die geneigt sind und am First miteinander verbunden sind. Die Sparren sind statisch gesehen Balken und haben in der Regel am unteren Ende ein Auflager und am obere Ende ein Gelenk zum anderen Sparren. Je nach Konstruktion können die Sparren auch auskragend sein, um einen Dachüberstand zu schaffen.

Es gibt es verschiedene Möglichkeiten, das Sparrendach auszuführen, was bedeutet, dass die verschiedenen Elemente mit unterschiedlichen Materialien und Systemen gebaut werden können.

Ein Beispiel ist in der obigen Abbildung zu sehen, in der ein Holzbalken als Deckenbalken gewählt wurde, der die horizontalen Auflagerkräfte der Sparren, auf Zug, aufnimmt. Als Alternative könnte auch eine Betonplatte verwendet werden.

Außerdem wird ein Stahl Windverband als Aussteifungssystem gewählt. Alternativ könnte man auch Platten wie OSB-Platten verwenden.

Sparrenarten

Normale Sparren

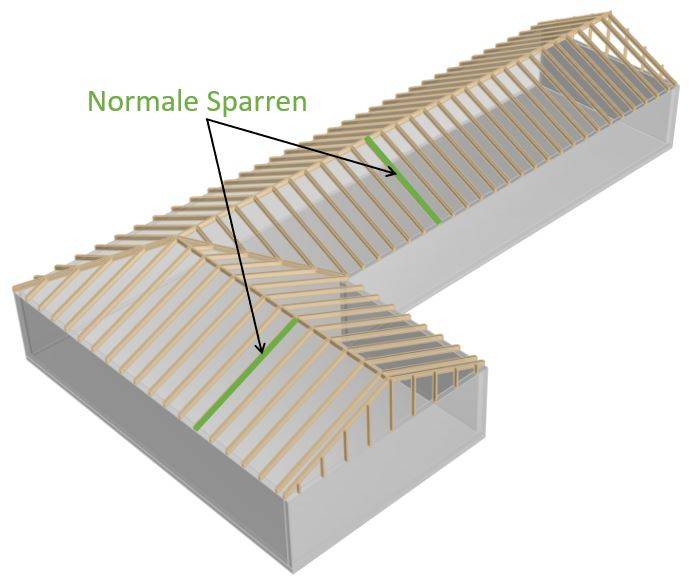
Die normalen Sparren sind geneigte Teile des Sparrendachs, die zwischen First und den Wänden gestützt werden. Diese Sparren sind in gleichem Abstand angeordnet und tragen den Dachaufbau und die Dachlasten.

Kehlsparren

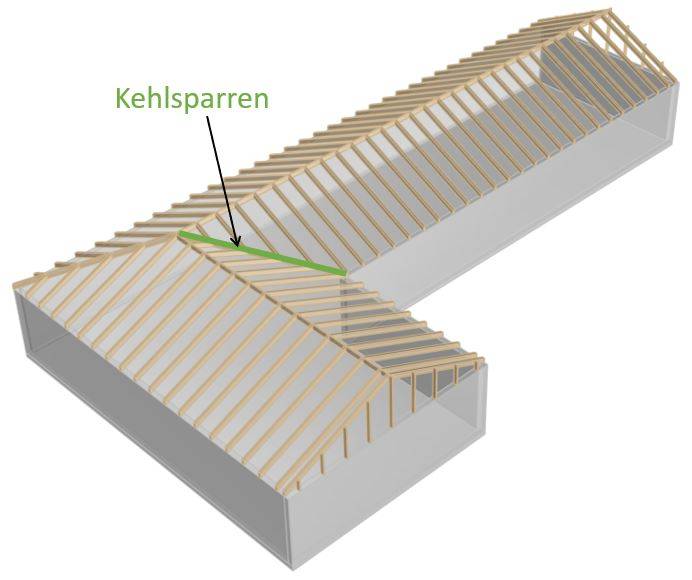
Kehlsparren werden dort angebracht, wo sich zwei Dachebenen kreuzen. Diese Sparren verlaufen diagonal von den Wänden zum First und stützen die Sparren, die senkrecht zum First verlaufen.

Kehlsparren haben in der Regel einen größeren Querschnitt, da sie eine größere Last tragen.

Gratsparren

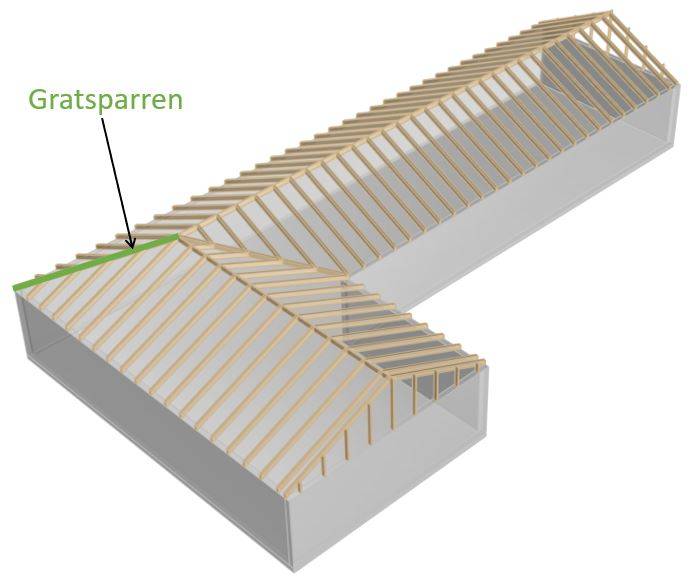
Die Gratsparren verlaufen von den äußeren Ecken diagonal vom Schnittpunkt zweier Wände bis zum Schnittpunkt des Firstes.

Wie die Kehlsparren stützen die Gratsparren die senkrecht zum First verlaufenden Dachsparren. Auch die Gratsparren haben einen größeren Querschnitt als die üblichen Sparren, da sie mehr Last tragen.

First

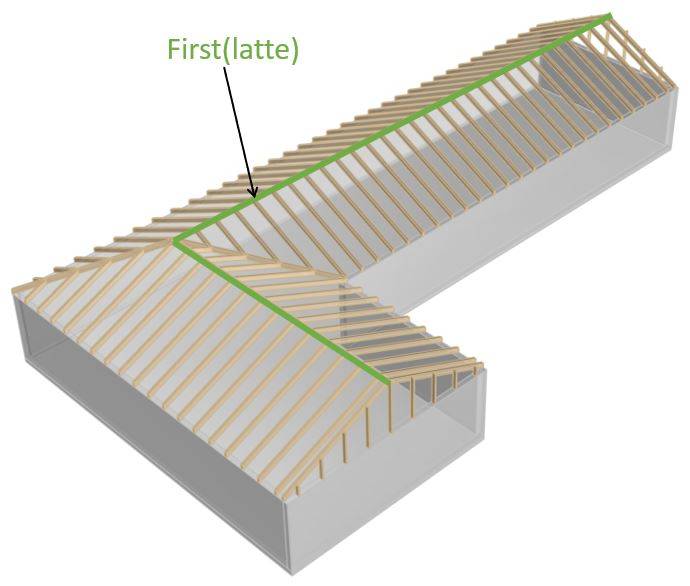
Der First ist das höchste horizontale Element eines Sparrendachs. Der First ist der Punkt, an dem sich die beiden geneigten Sparren treffen.

Oft wird das Sparrendach ohne Firstbalken ausgeführt.

Schiftersparren

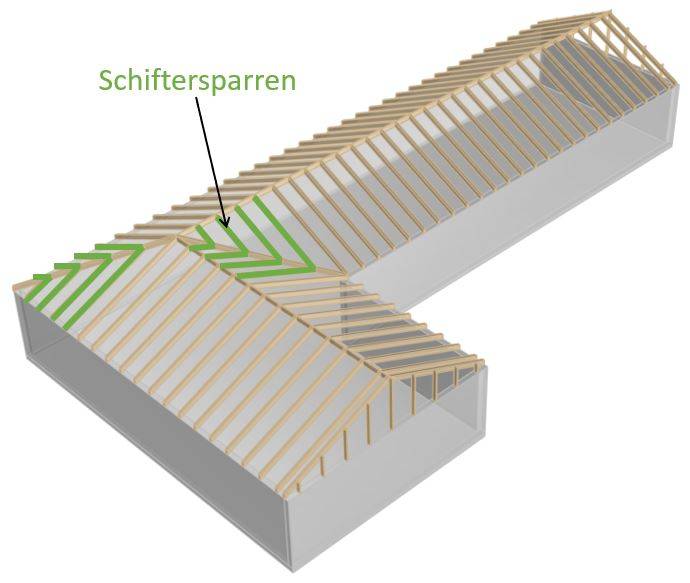
Schiftersparren spannen vom First bis zum Grat-/Kehlsparren und sind in der Regel kürzer als normale Sparren.

Statisches System des Sparrendach

Das statische System des Sparrendachs besteht aus 2 geneigten Sparren, die als Balken modelliert und am First mit einem Gelenk miteinander verbunden sind.

Die beiden Auflager werden als Festlager modelliert.

Das statische System des Sparrendaches ist in der nächsten Abbildung visualisiert. ⬇️⬇️

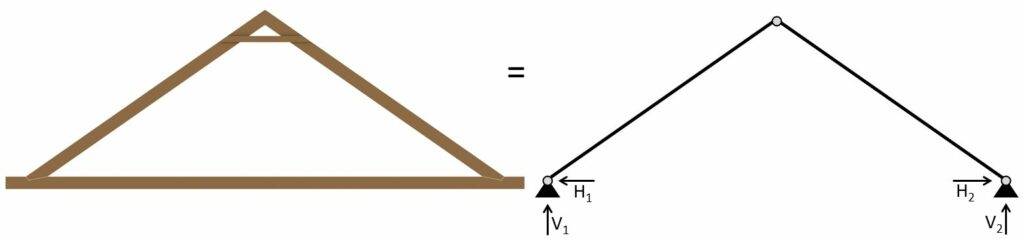
Um den Zusammenhang nicht zu verlieren, stellt das statische 2D-System die folgenden Dachsparren dar. 👇👇

Das Sparrendach kann natürlich auch andere Grundrisse mit größeren Spannweiten oder steilerer Neigung haben.

Charakteristische Lasten – Sparrendach

Die Lasten werden in diesem Artikel nicht abgeleitet. Die Berechnung von Eigen-, Nutz-, Wind– und Schneelasten für geneigte Dächer haben wir in früheren Artikeln ausführlich erläutert.

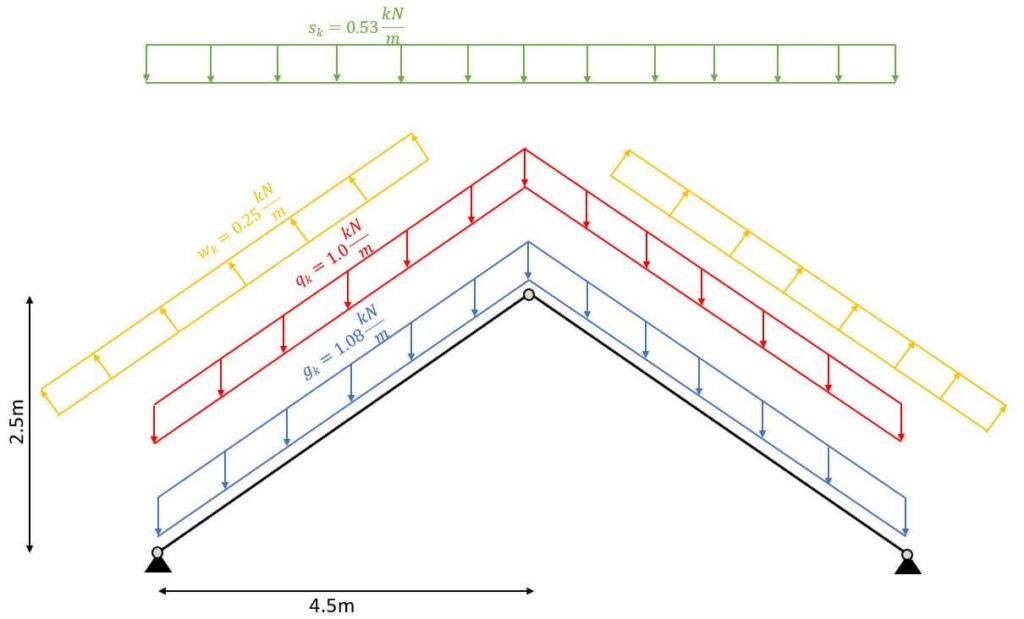
Für die Bemessung der Dachsparren werden wir die folgenden Lastannahmen verwenden:

gk	1.08 kN/m2	Charackteristischer Wert der Eigenlast
qk	1.0 kN/m2	Charackteristischer Wert der Nutzlast
sk	0.53 kN/m2	Charackteristischer Wert der Schneelast

Wie wir auch im Artikel über die charakteristische Schneelast besprochen haben, gibt es 3 verschiedene Lastfälle, bei denen nur die Hälfte des Wertes auf einer Schrägseite, aber der volle Wert auf der anderen Seite angesetzt wird.

Der Einfachheit halber betrachten wir in diesem Artikel jedoch nur Lastfall 1, bei dem s_k = 0,53 kN/m² auf beide Sparren wirkt.

In diesem Blogpost betrachten wir nur den äußeren Winddruck für Flächen von 10 m².

Wind Richtung Vorne

wk.F	-0.25(/0.35) kN/m2	Charackteristischer Wert der Windfläche F
wk.G	-0.25(/0.35) kN/m2	Charackteristischer Wert der Windfläche G
wk.H	-0.1(/0.2) kN/m2	Charackteristischer Wert der Windfläche H
wk.I	-0.2(/0.0) kN/m2	Charackteristischer Wert der Windfläche I
wk.J	-0.25(/0.0) kN/m2	Charackteristischer Wert der Windfläche J

Wind Richtung Seite

wk.F	-0.55 kN/m2	Charackteristischer Wert der Windfläche F
wk.G	-0.7 kN/m2	Charackteristischer Wert der Windfläche G
wk.H	-0.4 kN/m2	Charackteristischer Wert der Windfläche H
wk.I	-0.25 kN/m2	Charackteristischer Wert der Windfläche I

Der Einfachheit halber verwenden wir in diesem Tutorial nur die Windlast von der Seite. Daher wird die Windlast w_k.I = -0,25 kN/m² auf beide Sparren aufgebracht.

Last Kombinationen – Sparrendach

Glücklicherweise haben wir bereits einen ausführlichen Artikel darüber geschrieben, was Lastkombinationen sind und wie wir sie verwenden. Falls Du es noch einmal nachlesen möchtest, kannst Du den Blogbeitrag hier lesen.

Wir haben uns dafür entschieden, w_k.I = -0,25 kN/m² als Windlast in die Lastkombinationen einzubeziehen, da dies die Windlast ist, die auf den von uns betrachteten Abschnitt wirkt, und um die Berechnung einfacher zu halten.

Im Prinzip solltest Du alle Lastfälle berücksichtigen. Mit etwas mehr Erfahrung kannst du jedoch einige der Werte ausschließen.

In modernen FE-Programmen können mehrere Werte für die Windlast angesetzt werden und Lastkombinationen werden automatisch generiert. Der Computer ist uns also eine große Hilfe. 🧑‍💻👍

ULS Last Kombinationen

Falls du zum ersten Mal Lastkombinationen berechnest, weißt du vielleicht wie die verschiedenen Lasten auf einen schrägen Balken angesetzt werden, aber wir haben einen ganzen Artikel darüber geschrieben.

Die folgenden Lastkombinatinen verwenden die Sicherheitsfaktoren des Eurocodes. Im nationalen Anhang deines Landes sind diese eventuell anderst definiert.

LK1	$1.35 \cdot 1.08 \frac{kN}{m^2} $
LK2	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2}$
LK3	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 0.53 \frac{kN}{m^2}$
LK4	$1.35 \cdot 1.08 \frac{kN}{m^2} + 0 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 1.5 \cdot 0.53 \frac{kN}{m^2}$
LK5	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 0.53 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-0.25 \frac{kN}{m^2}) $
LK6	$1.35 \cdot 1.08 \frac{kN}{m^2} + 0 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 1.5 \cdot 0.53 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-0.25 \frac{kN}{m^2}) $
LK7	$1.35 \cdot 1.08 \frac{kN}{m^2} + 0 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 0.53 \frac{kN}{m^2} + 1.5 \cdot (-0.25 \frac{kN}{m^2}) $
LK8	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 0.53 \frac{kN}{m^2} $
LK9	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot (-0.25 \frac{kN}{m^2}) $
LK10	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-0.25 \frac{kN}{m^2}) $
LK11	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot (-0.25 \frac{kN}{m^2}) + 0.7 \cdot 1.5 \cdot 0.53 \frac{kN}{m^2} $
LK12	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 0.53 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-0.25 \frac{kN}{m^2})$

Du kannst auch unseren kostenlosen Lastkombinationen-Generator verwenden, um alle ULS-Lastkombinationen automatisch zu erstellen.

Charakteristische SLS Last Kombinationen

LC1	$1.08 \frac{kN}{m^2} $
LC2	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2}$
LC3	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.7 \cdot 0.53 \frac{kN}{m^2}$
LC4	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.6 \cdot (-0.25 \frac{kN}{m^2})$
LC5	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.7 \cdot 0.53 \frac{kN}{m^2} + 0.6 \cdot (-0.25 \frac{kN}{m^2}) $
LC6	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + 0.53 \frac{kN}{m^2} + 0.6 \cdot (-0.25 \frac{kN}{m^2}) $
LC7	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 0.53 \frac{kN}{m^2} + (-0.25 \frac{kN}{m^2}) $
LC8	$1.08 \frac{kN}{m^2} + 0.53 \frac{kN}{m^2}$
LC9	$1.08 \frac{kN}{m^2} + (-0.25 \frac{kN}{m^2}) $
LC10	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.6 \cdot (-0.25 \frac{kN}{m^2}) $
LC11	$1.08 \frac{kN}{m^2} + (-0.25 \frac{kN}{m^2}) + 0.7 \cdot 0.53 \frac{kN}{m^2} $
LC12	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + 0.53 \frac{kN}{m^2}$
LC13	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + (-0.25 \frac{kN}{m^2})$

Sparren Holz Material Eigenschaften

Für diesen Blogbeitrag/dieses Tutorial wählen wir ein Konstruktionsholz C24.

Die folgenden charakteristischen Festigkeits- und Steifigkeitsparameter wurden online von einem Hersteller gefunden.

Biegefestigkeit fm.k	24 N/mm2
Zugfestigkeit parallel zur Holzfaser ft.0.k	14 N/mm2
Zugfestigkeit rechtwinklig zur Holzfaser ft.90.k	0.4 N/mm2
Druckfestigkeit parallel zur Holzfaser fc.0.k	21 N/mm2
Druckfestigkeit rechtwinklig zur Holzfaser fc.90.k	2.5 N/mm2
Schubfestigkeit fv.k	4.0 N/mm2
E-modul E0.mean	11.0 kN/mm2
E-modul E0.g.05	7.4 kN/mm2

K_mod Faktor

Falls du nicht genau weißt, was der k_mod Faktor ist, haben wir in einem anderen Artikel eine Erklärung dazu geschrieben, die Du nachlesen kannst.

Da wir alles so kurz wie möglich halten wollen, werden wir ihn in diesem Artikel nicht wiederholen – wir definieren nur die Werte von k_mod.

Für ein Wohnhaus, das nach EN 1995-1-1 2.3.1.3 in die Nutzungsklasse 1 eingestuft ist, ergeben sich die folgenden Belastungsdauern für die verschiedenen Lasten.

Eigenlast	Ständig
Nutzlast	Mittel
Schnee- und Windlast	Kurz

Jetzt können wir die Werte für k_mod und Konstruktionsholz C24 mithilfe EN 1995-1-1 Tabelle 3.1 ermitteln.

Eigenlast	Stöndige Einwirkung	Nutzungsklasse 1	0.6
Nutzlast	Mittlere Einwirkung	Nutzungsklasse 1	0.8
Schnee- und Windlast	Kurze Einwirkung	Nutzungsklasse 1	0.9

Teilsicherheitsbeiwert $\gamma_{M}$

Nach EN 1995-1-1 Tabelle 2.3 ist der Teilsicherheitsfaktor $\gamma_{M}$ definiert als

$$\gamma_{M} = 1.3$$

Definition der Querschnittshöhe und -breite

Bevor wir nun endlich mit der Statik der Sparren beginnen können, müssen wir die Breite und Höhe des Querschnitts festlegen. Dies beruht auf der Erfahrung des Statikers.

Breite	w = 100 mm
Höhe	h = 240 mm

Wenn wir die Höhe und Breite des Querschnitts kennen, können wir die Trägheitsmomente berechnen, die für die Berechnung der Biegespannung erforderlich sind.

$$I_{y} = \frac{w \cdot h^3}{12} = \frac{100mm \cdot (240mm)^3}{12} = 1.152 \cdot 10^8 mm^4 $$

$$I_{z} = \frac{w^3 \cdot h}{12} = \frac{(100mm)^3 \cdot 240mm}{12} = 2.0 \cdot 10^7 mm^4 $$

ULS Design

Bei der ULS (ultimate limit state) Bemessung werden die Spannungen im Sparren aufgrund von Biegemoment und Querkraft nachgewiesen. Außerdem werden wir, aufgrund der Druckkraft im Sparren, Knicken nachweißen.

Du kannst dir unser YouTube-Video-Tutorial über die Bemessung von Holzelementen ansehen. 👇👇

Um die Spannungen der Sparren zu berechnen, müssen wir die Biegemomente, Normal- und Querkräfte aufgrund verschiedener Lasten berechnen. Zur Ausführung dieser Aufgabe wird ein FE- oder Balkenprogramm verwendet.

Berechnung des Biegemoments, der Normal- und Schubkraft

Lastkombination 3 mit der Verkehrslast als dominierende und der Schneelast als reduzierte Last führt zu den höchsten Schnittgrößen, die wir visualisieren im folgenden visualisieren. 👇👇

Last Kombination 3 – Lasten

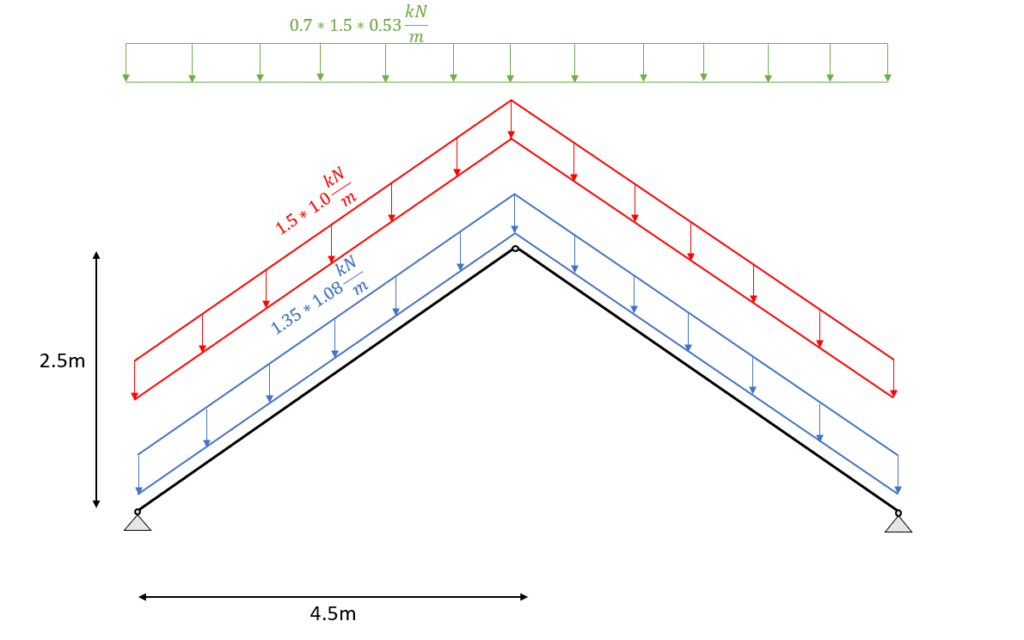
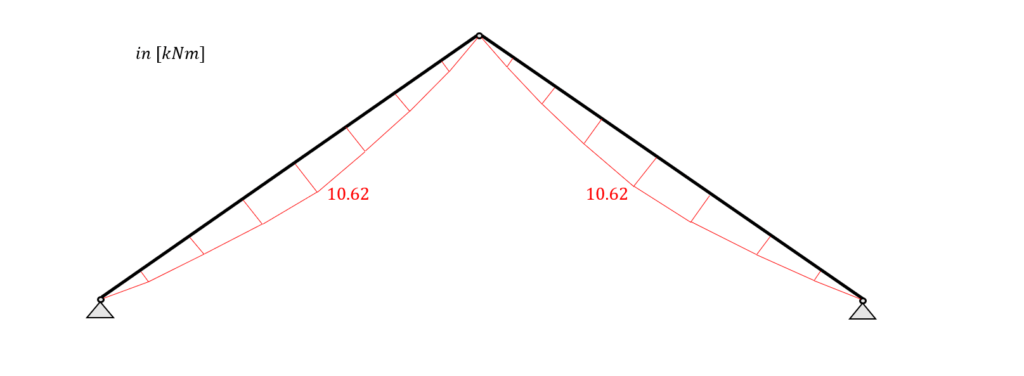
Last Kombination 3 – Biegemomente

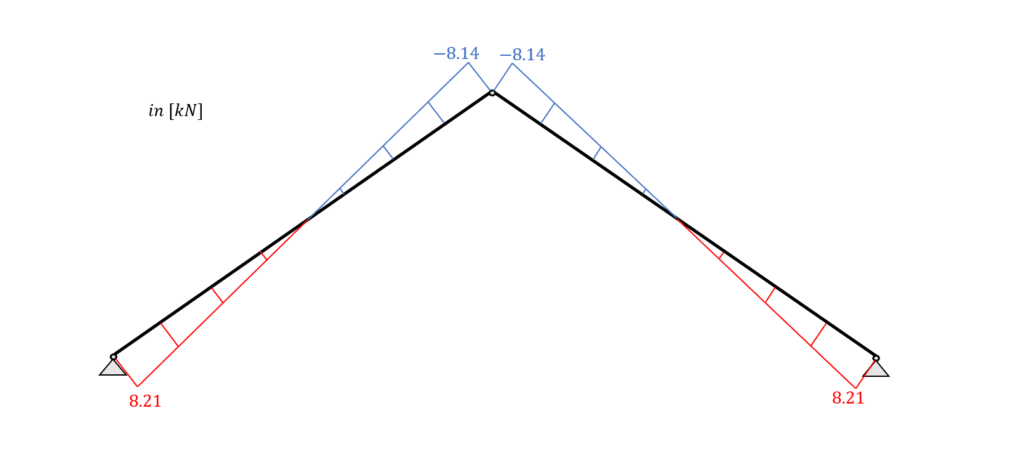
Last Kombination 3 – Schubkräfte

Last Kombination 3 – Normalkräfte

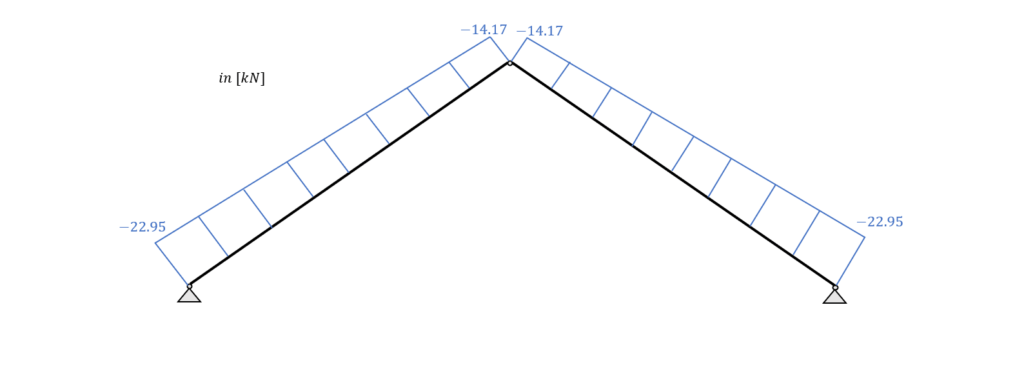
Aus dem Normalkraftdiagram wird ersichtlich, dass durch in Lastkombination LK3 jedes Element des Sparrensystems auf Druck wirkt.

Biege und Druck Nachweis – Sparren

Aus dem maximalen Biegemoment (10,62 kNm) und der Druckkraft $(\frac{14,17kN + 22,95kN}{2}=18,56kN)$ an der gleichen Stelle können wir die Spannung im kritischsten Querschnitt berechnen.

Biegespannung:	$\sigma_{m} = \frac{M_{d}}{I_{y}} \cdot \frac{h}{2} = \frac{10.62 kNm}{1.152 \cdot 10^{-4}} \cdot \frac{0.24m}{2} = 11.06 MPa$
Druckspannung:	$\sigma_{c} = \frac{N_{d}}{w \cdot h} = \frac{18.56 kN}{0.1m \cdot 0.24m} = 0.773 MPa$
Widerstandsspannungen:	$f_{d} = k_{mod} \cdot \frac{f_{k}}{\gamma_{m}}$
Biegewiderstandsspannung (M-Einwirkung):	$k_{mod.M} \cdot \frac{f_{m.k}}{\gamma_{m}} = 14.8 MPa$
Druckwiderstandsspannung (M-action):	$k_{mod.M} \cdot \frac{f_{c.k}}{\gamma_{m}} = 12.9 MPa$
Ausnutzung nach EN 1995-1-1 (6.19):	$\eta = (\frac{\sigma_{c}}{f_{c.d}})^2 +  \frac{\sigma_{m}}{f_{m.d}} = 0.75 < 1.0$

Schub Nachweis – Sparren

Aus der maximalen Querkraft (Auflager: 8,21 kN) lässt sich die Schubspannung im kritischsten Querschnitt berechnen.

Schubspannung	$\tau_{d} = \frac{3V}{2 \cdot w \cdot h} =  \frac{3 \cdot 8.21 kN}{2 \cdot 0.1m \cdot 0.24m} = 0.513 MPa$
Schubwiderstandsspannung	$f_{v} = k_{mod.M} \cdot \frac{f_{v}}{\gamma_{m}} = 2.46 MPa$
Ausnutzung nach EN 1995-1-1 (6.13):	$\eta = \frac{\tau_{v}}{f_{v}} = 0.21 < 1.0$

Knicken Nachweis

Wir gehen davon aus, dass ein Ausknicken aus der Ebene (z-Richtung) vernachlässigt werden kann, da die Sparren an den Seiten von den Dachplatten wie OSB-Platten gehalten werden.

Als erstes, definieren wir die Knicklänge l_y als:

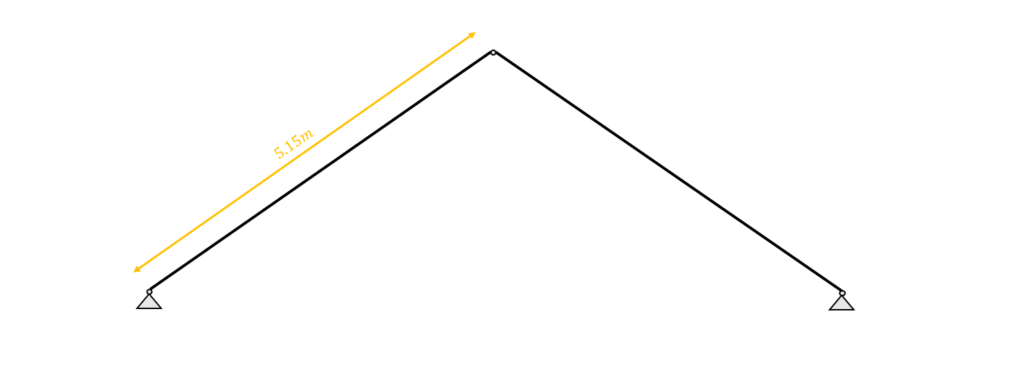
Trägheitsmoment	$l_{y} = 5.15m$
Trägheitsradius	$i_{y} = \sqrt{\frac{I_{y}}{w \cdot h}} = 0.069m$
Schlankheitsgrad	$\lambda_{y} = \frac{l_{y}}{i_{y}} = 74.334$
Relativer Schlankheitsgrad (EN 1995-1-1 (6.21))	$ \lambda_{rel.y} = \frac{\lambda_{y}}{\pi} \cdot \sqrt{\frac{f_{c.0.k}}{E_{0.g.05}}}  = 1.26$
$\beta_{c}$ Faktor (EN 1995-1-1 (6.29))	$\beta_{c} = 0.2$
ky Faktor (EN 1995-1-1 (6.27))	$k_{y} = 0.5 \cdot (1+ \beta_{c} \cdot (\lambda_{rel.y} – 0.3) + \lambda_{rel.y}^2) = 1.39$
Knickbeiwert (EN 1995-1-1  (6.25))	$k_{c.y} = \frac{1}{k_{y} + \sqrt{k_{y}^2 – \lambda_{rel.y}^2}} = 0.51$
Ausnutzung (EN 1995-1-1 (6.23))	$\frac{\sigma_{c}}{k_{c.y} \cdot f_{c.d}} + \frac{\sigma_{m}}{f_{m.d}} = 0.87 < 1$

SLS Nachweis

In einem anderen Artikel erklären wir ausführlich das SLS-Design. In diesem Blogbeitrag erklären wir nicht alles im Detail, sondern zeigen die Berechnungen.

Anfangsdurchbiegung u_inst

Die u_inst (Anfangsdurchbiegung) der Sparren wird mit der Last der charakteristischen Lastkombination berechnet.

Wie bei den Biegemomenten, Schub- und Axialkräften verwenden wir ein FE-Programm, um die Durchbiegungen infolge unserer Lastkombinationen zu berechnen.

LK3 der charakteristischen Lastkombinationen führt zu der größten Durchbiegung u.

$$u_{inst} = 15.9 mm$$

EN 1995-1-1 Tabelle 7.2 empfiehlt Werte für die Durchbiegung nur für „Einfeldträger“ und „auskragende Balken“ und nicht für ein Sparrensystem wie in diesem Fall.

Die Grenzwerte für die Durchbiegung können jedoch mit dem Bauherrn vereinbart werden, und das Tragwerk stürzt nicht aufgrund zu großer Durchbiegungen ein, wenn der Sparren für alle ULS-Berechnungen nachgewiesen wird.

Da die Biegemoment- und Schubkraftverteilung des Sparrendachs der eines Einfeldträgers entspricht, verwenden wir in dieser Berechnung den Wert für „Einfeldträger“ aus EN 1995-1-1 Tabelle 7.2.

$$w_{inst} = l/300 = 5.15m/300 = 17.17 mm$$

Ausnutzung

$$\eta = \frac{u_{inst}}{w_{inst}} =  \frac{15.9mm}{17.17mm} = 0.92 < 1$$

Enddurchbiegung u_fin

Die Enddurchbiegung u_fin unseres Trägers/Sparrens kann durch Addition der Kriechverformung u_creep zur Anfangsdurchbiegung u_inst berechnet werden.

Daher werden wir die Kriechverformung mit einem FE-Programm berechnen. Das geht vielleicht ein bisschen schnell, aber wir haben die Grundlagen bereits in dem Artikel über die Bemessung von Holzbalken behandelt.

Schau am besten dort nach, wenn Du genau wissen willst, wie man u_creep berechnet.

Die Kriechverformung von LK3 wird wie folgt berechnet:

$$u_{creep} = 4.8mm$$

Addiert man das Kriechen zur Anfangsdurchbiegung, erhält man die Enddurchbiegung.

$$u_{fin} = u_{inst} + u_{creep} = 15.9mm + 4.8mm= 20.7mm$$

Grenzwert von u_fin nach EN 1995-1-1 Table 7.2:

$$w_{fin} = l/150 = 5.15m/150 = 34.3 mm$$

Ausnutzung:

$$\eta = \frac{u_{fin}}{w_{fin}} =  \frac{20.7mm}{34.3mm} = 0.6$$

Fazit

Nachdem nun die Sparren auf Druck, Biegung, Knickung und Durchbiegung geprüft sind, können wir endlich sagen, dass die Querschnittshöhen und -breiten nachgewiesen sind – check. ✔️✔️

Es ist interessant, den Unterschied in den Querschnittseigenschaften zwischen dem Sparrendach und dem Kehlbalkendach zu sehen, oder?

Wir haben in beiden Tragwerken die gleiche Spannweite und Neigung verwendet, was dazu führt, dass die Sparren beim Sparrendach 240 mm hoch sind, während sie beim Kehlbalkendach 160 mm hoch sind.

Aber beim Kehlbalkendach gibt es ein zusätzliches Element – den Kehlbalken.

Jetzt bin ich sehr daran interessiert, von Dir zu hören: Bevorzugst Du das Sparrendach oder das Kehlbalkendach? Was sind die Vor- und Nachteile der beiden Tragwerke? Lass es uns in den Kommentaren unten wissen. ✍️✍️