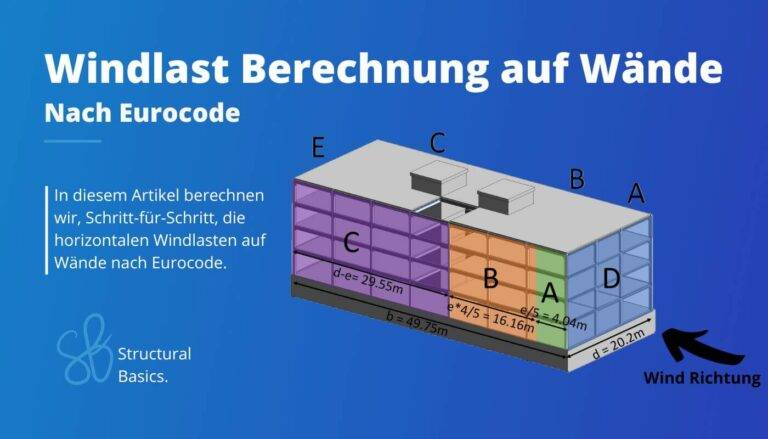
Die 5 Lasten Auf Dächern [Überblick]

Auf Dächer sind unterschiedlichen Lasten ausgesetzt, die mit einer statischen Berechnung nachgewiesen werden müssen. In diesem Artikel schauen wir uns alle 5 Lasten auf Dächer genauer an.
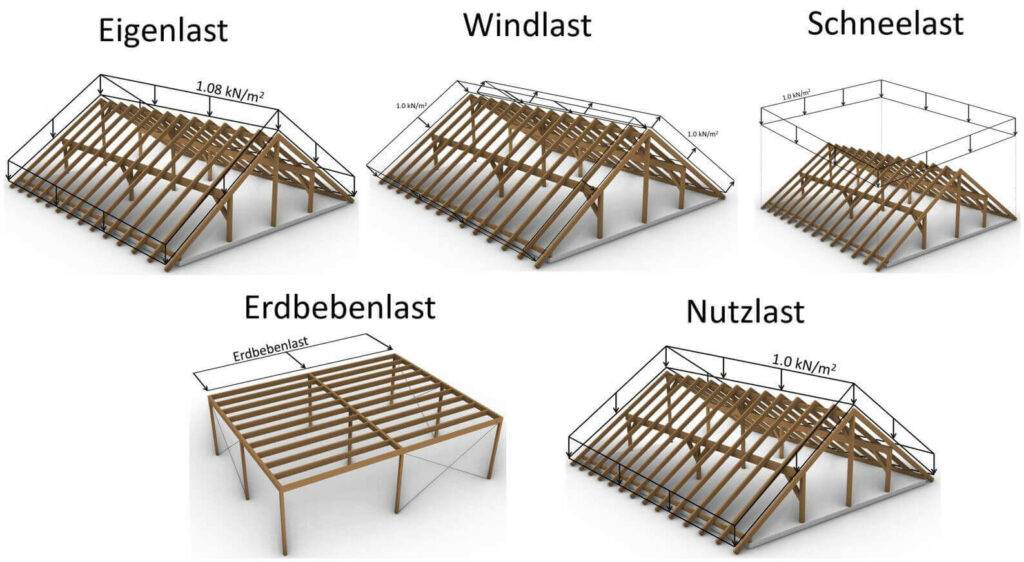
Wir werden jede Last kurz erklären, aufzeigen wie man die Last auf ein statisches System ansetzt und kurz aufzeigen bzw. auf andere Ressourcen verweisen, die zeigen wie man diese Lasten berechnen kann.
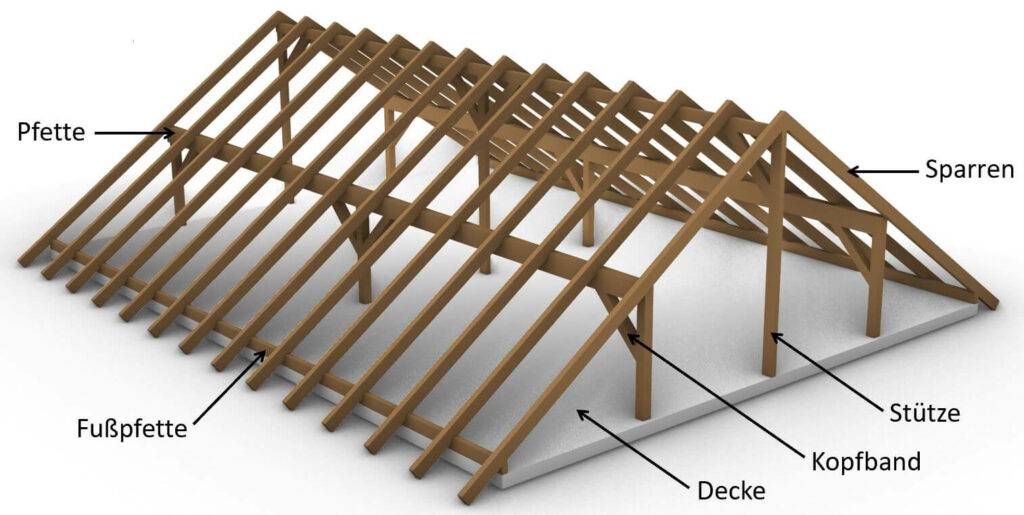
Alles wird anhand des Pfettendachs praxisnah aufgezeigt. 👇👇
Let’s get started. 😄👍
1. Eigenlast
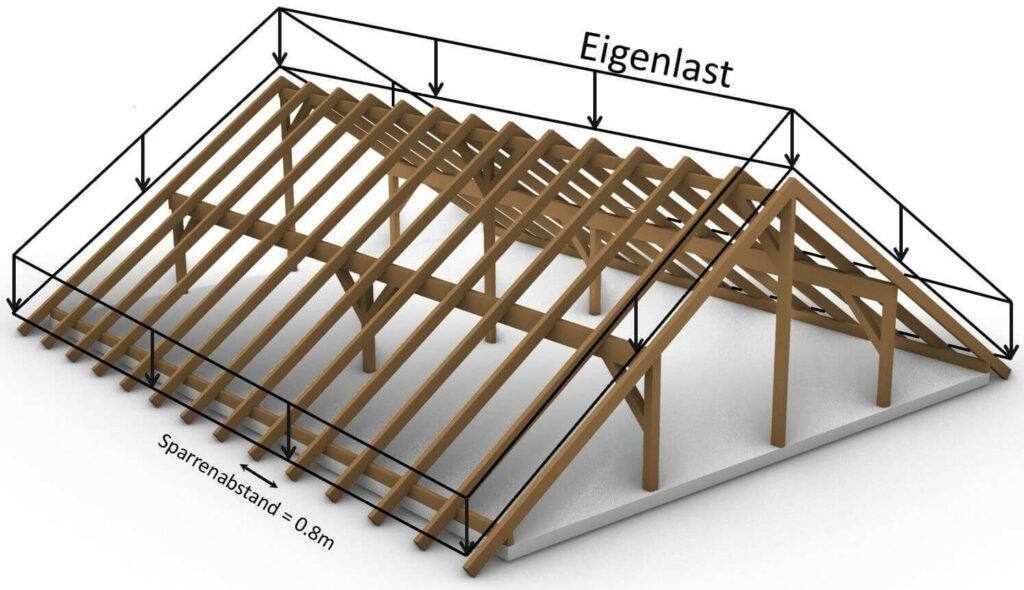
Die Eigenlast ist das (Eigen-) gewicht aller Elemente, die auf das Bauwerk einwirken. Dazu gehören tragende und nicht-tragende Elemente.
Beispiele von tragenden Bauteilen:
- Pfette
- Sparren
- Stütze
- Wand
Beispiele von nicht-tragenden Bauteilen:
- Dämmung
- Dachlatten
- Dachziegel
- etc.
Um eine Flächenlast oder eine Linienlast zu erhalten, die wir dann auf die Dachfläche bzw. die Sparren ansetzen können, müssen wir die Dichte und die Abmessungen jedes Elements definieren.
Die Flächenlast wird berechnet als:
$$\mbox{Flächeneigenlast} = \mbox{Dichte} \, \cdot \mbox{Dicke} $$
Die Eigenlast des Pfettendach, kann vereinfacht gerechnet werden als: 👇👇
| Element | Dicke [mm] | Dichte [kg/m3] | Flächenlast [kN/m2] |
|---|---|---|---|
| OSB Platte | 20 | 650 | 0.13 |
| Isoliering | 300 | 100 | 0.3 |
| Dachziegel | 0.65 | ||
| Summe | 1.08 |
Beispielrechnung einer OSB Platte
$$650 \frac{kg}{m^3} \cdot 0.02 m = 0.13 \frac{kN}{m^2} $$
Lastrichtung
💡
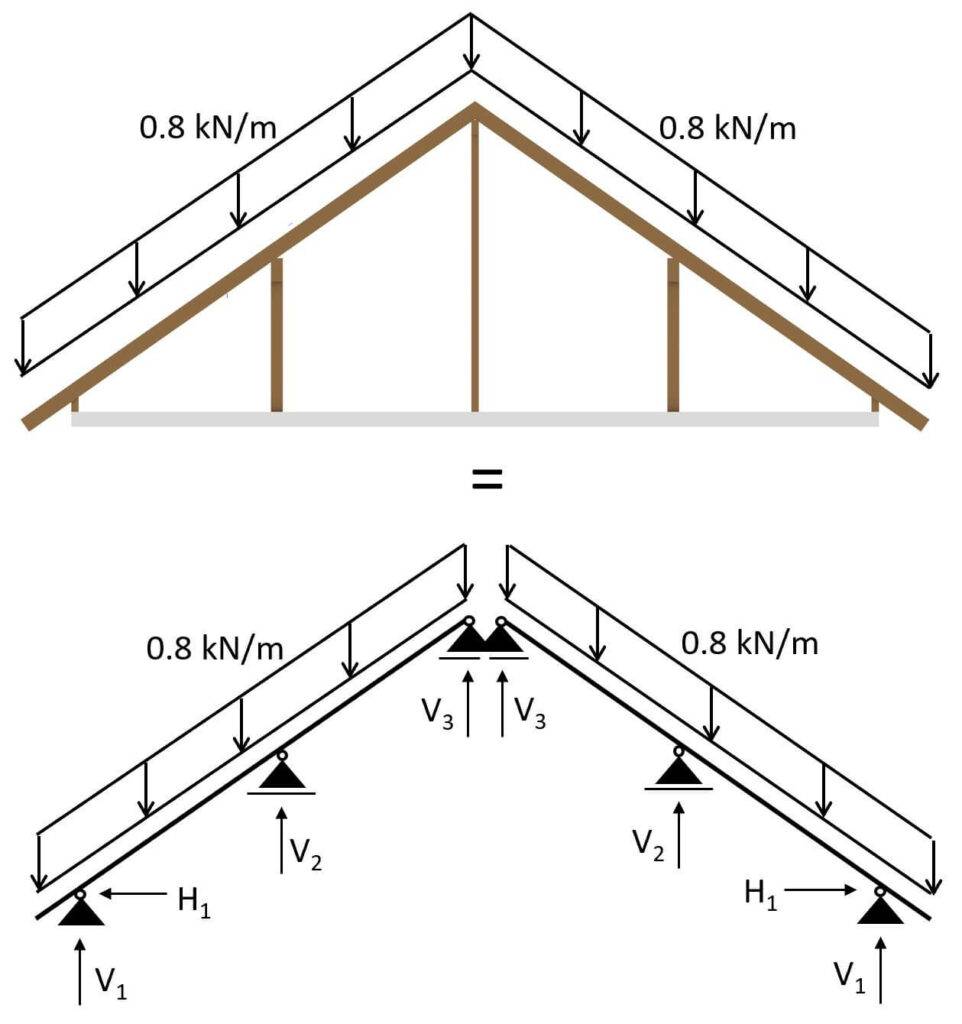
Die Richtung der Last ist sehr wichtig. Für die Eigenlast ist die Richtung immer die z-Achse nach unten, und sie wird entlang der Neigung der Sparren verteilt.
Eigenlast in 3D System
Die Summe der Eigenlast kann in 3D-FEM Programmen (RFEM, Robot, etc.) direkt auf das Tragwerk angesetzt werden. In diesen Programmen werden dann die Flächenlasten automatisch in Linienlasten auf die Sparren umgerechnet.
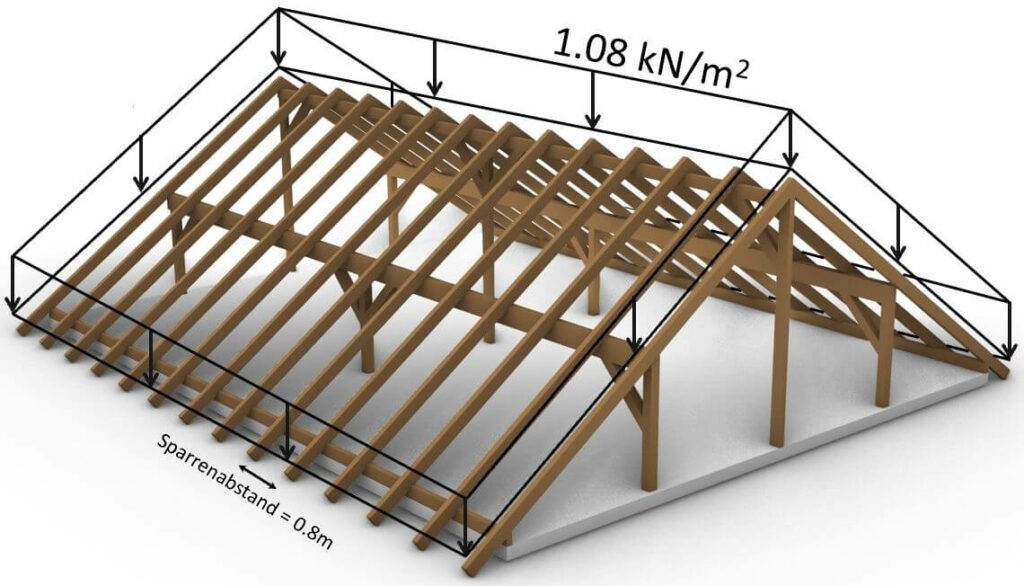
Eigenlast in 2D System
Alternativ, falls man die Statik per Hand oder mit einem 2D Statikprogram rechnet, dann kann man selber die Flächenlast in eine Linienlast umrechnen. ⬇️⬇️
$$\mbox{Flächeneigenlast} \, \cdot \mbox{Sparrenabstand} = \mbox{Linieneigenlast}$$
In unserem Beispiel ergibt das eine Linienlast von:
$$1.08 \frac{kN}{m^2} \cdot 0.8 m = 0.86 \frac{kN}{m} $$
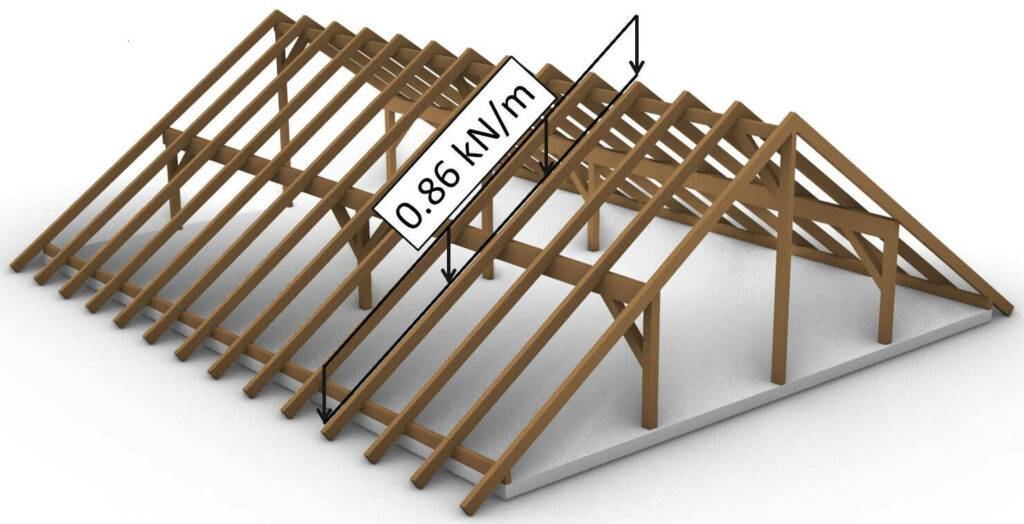
Dann müssen wir noch das Eigengewicht der Sparren dazurechnen.
$$\mbox{Sparreneigenlast} = \frac{\mbox{Sparren Dichte}}{100} \, \cdot \mbox{Querschnittshöhe} \cdot \mbox{Querschnittsbreite}$$
Für Konstruktionsholz C24 ergibt das eine Last von:
$$350 \frac{kg}{m^3} \cdot 0.2 m \cdot 0.1 m = 0.07 \frac{kN}{m} $$
Beide Linienlasten zusammengerechnet ergeben die Eigenlast in 2D.
$$ 0.864 \frac{kN}{m} + 0.07 \frac{kN}{m} = 0.93 \frac{kN}{m} $$
Diese Last können wir jetzt auf das 2D statische System ansetzen.
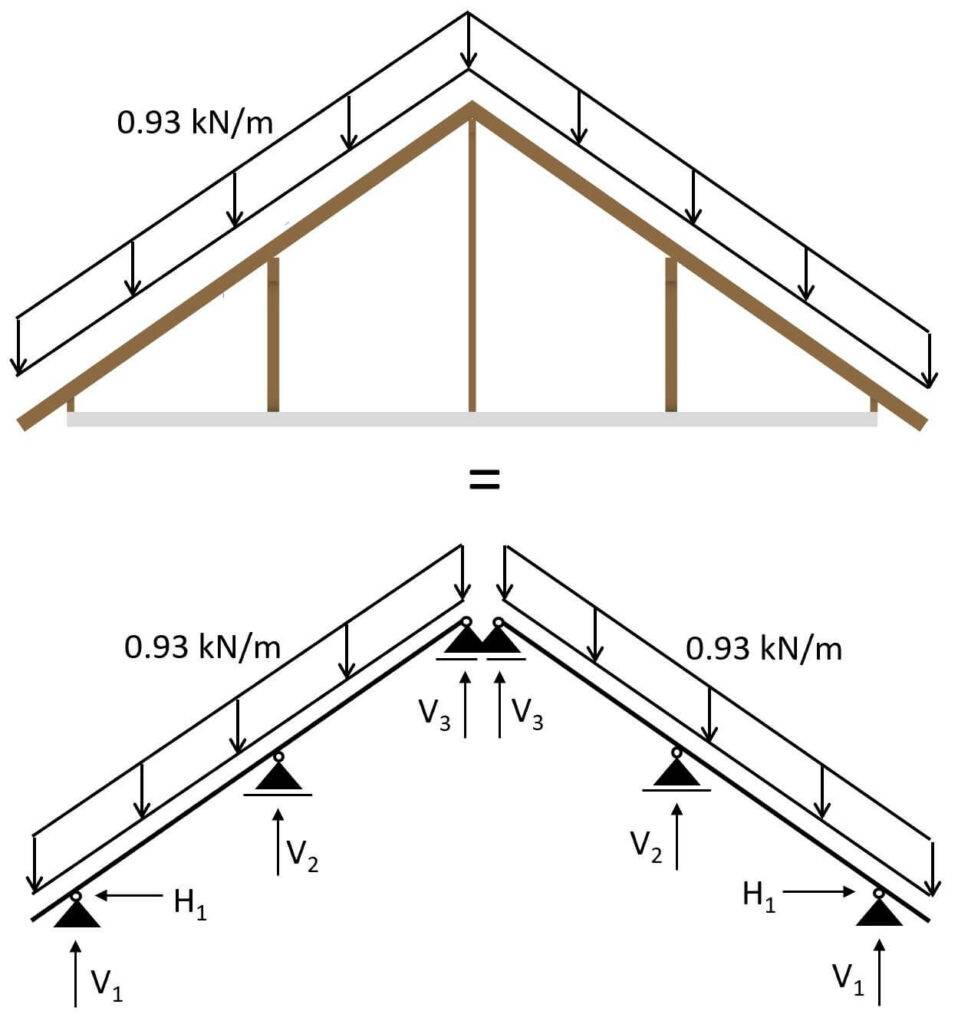
Als nächster Schritt können die Schnittkräfte berechnet werden. Danach kann der Querschnitt bemessen werden. 🪵🪵
2. Windlast
Die Windlast ist die resultierende Last des Windes, der auf ein Gebäude oder Tragwerk bläst. 🌬️🌬️
Die Berechnung der Windlast erfolgt nach Eurocode EN 1991-1-4.
Wir haben bereits detaillierte Schritt-für-Schritt Berechnungsanleitungen geschrieben für die Windlast auf
Lastrichtung
💡
Die Richtung der Windlast ist immer senkrecht zu einer Gebäudeoberfläche wie Fassaden, Wände, Fenster und Dächer.
Windlast in 3D System
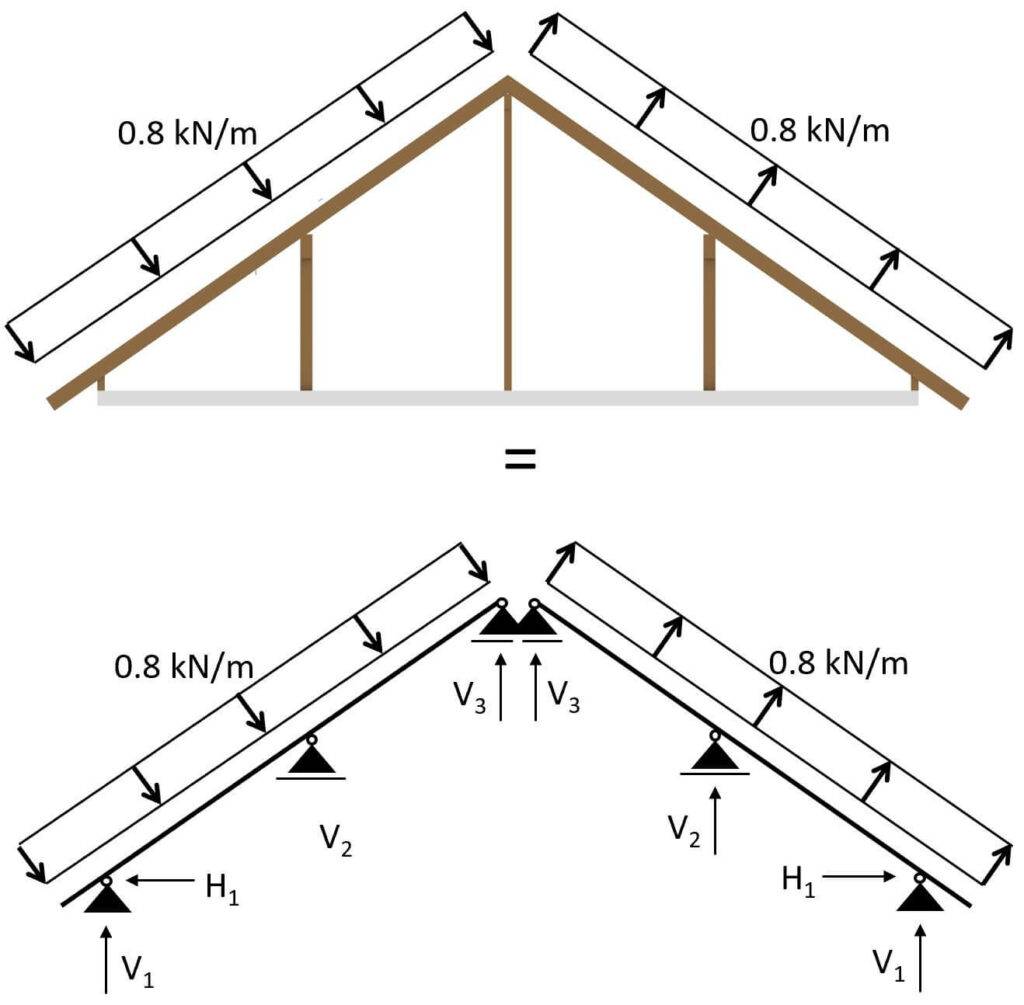
Die Windlast in der folgenden Abbildung ist stark vereinfacht. Normalerweise hat ein Dach verschiedene Bereiche mit unterschiedlichen Belastungswerten, aber der Zweck des Bildes ist es, die Belastungsrichtung senkrecht zu den Sparren zu visualisieren.
Wir gehen von einer Windlast von 1,0 kN/m2 aus, die gleichmäßig verteilt ist.
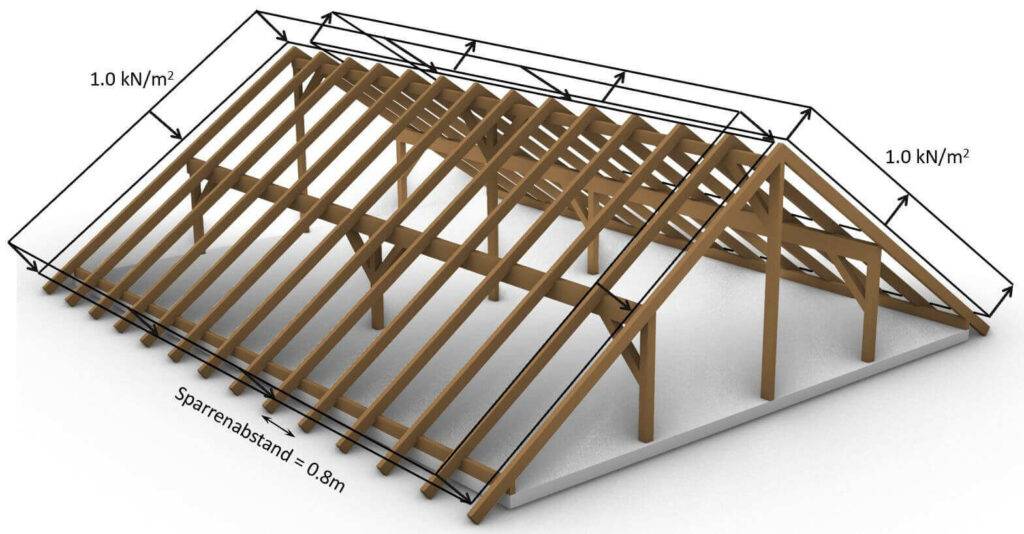
Windlast in 2D System
Wenn wir nun die Flächenlast wieder in eine Linienlast umwandeln wollen, dann multiplizieren wir die Flächenlast mit dem Abstand der Sparren:
$$1.0 \frac{kN}{m^2} \cdot 0.8 m = 0.8 \frac{kN}{m^2} $$
Und diese Linienlast kann nun in einem 2D-System angesetzt werden:
3. Schneelast
Die Schneelast ist die Kraft, die das Gewicht des Schnees repräsentiert und auf einer Fläche des Daches „liegt“.
Die Schneelast wird nach dem Eurocode EN 1991-1-3 berechnet.
Hier sind Schritt-für-Schritt Schneelast Berechnungsbeispiele für: 👇👇
Lastrichtung
Jetzt schauen wir uns an, wie die Schneelast auf Bauwerke aufgebracht wird. ➡️⬇️
💡
Die Richtung der Schneelast ist immer vertikal und wie bei der Eigenlast die z-Achse nach unten. ABER:
Die Schneelast folgt nicht der Neigung eines Bauwerks, sondern wird horizontal angesetzt. Das klingt kompliziert, ich weiß. Schauen wir uns also ein Beispiel an 😁⬇️.
Schneelast in 3D System
Als Beispiel verwenden wir eine Schneelast von 1,0 kN/m2, die für einige Tragwerke in Dänemark verwendet wird.
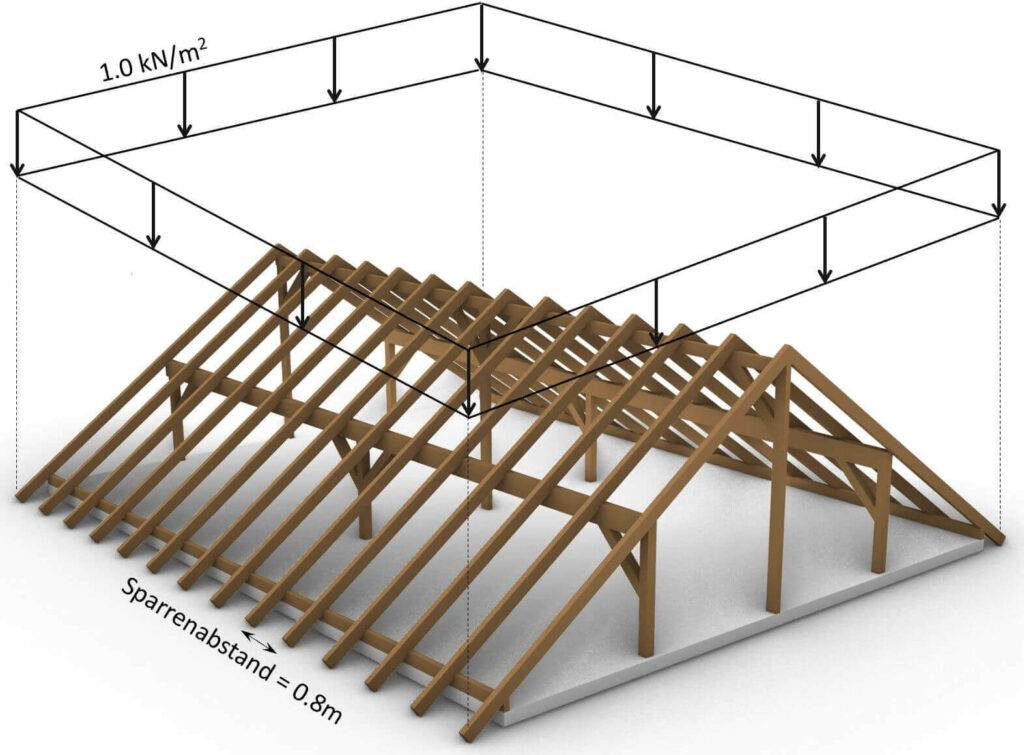
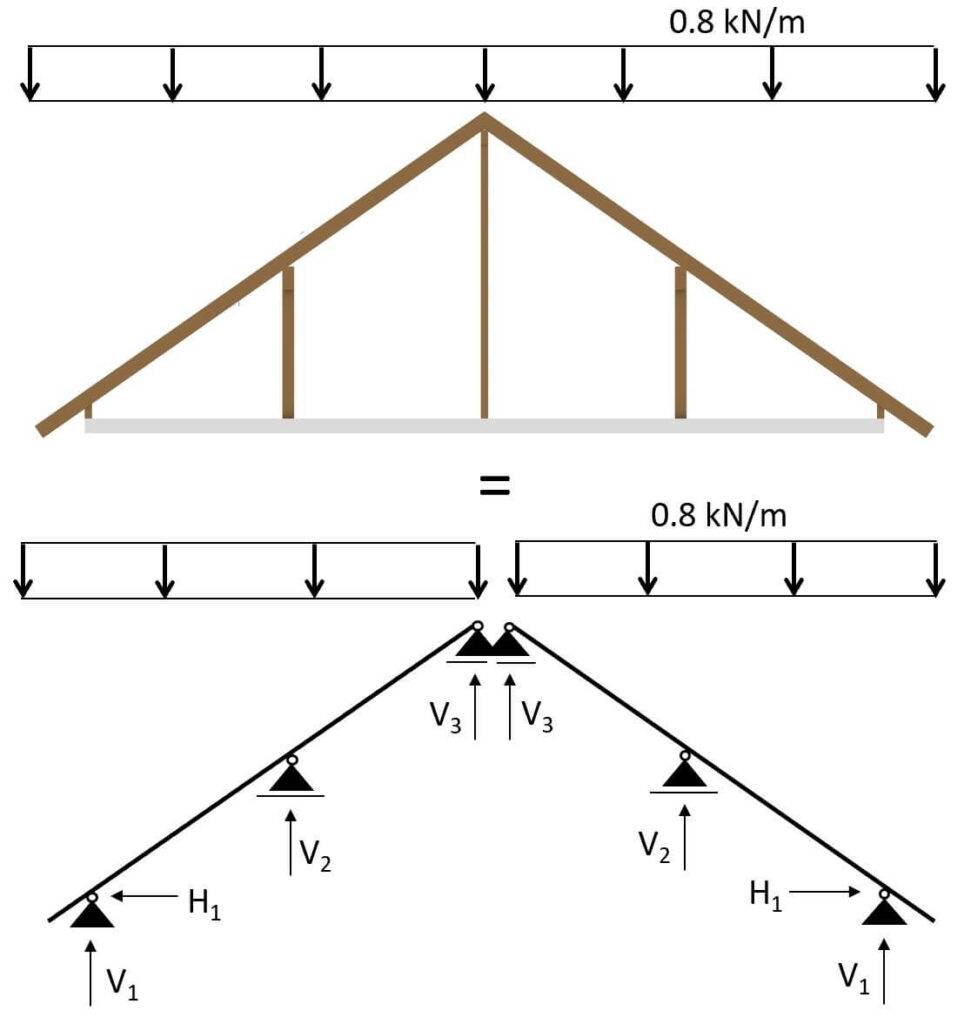
Schneelast in 2D System
$$1.0 \frac{kN}{m^2} \cdot 0.8 m = 0.8 \frac{kN}{m^2} $$
Diese Linienlast kann jetzt auf das 2D statisches System angebracht werden.
4. Nutzlast
Die Nutzlast ist die Kraft, die sich aus dem Gewicht von Dingen ergibt, die ihren Standort wechseln können, aber auch das Gewicht kann sich im Laufe der Zeit ändern. Die Nutzlast repräsentiert zum Beispiel Menschen oder Möbel in einem Gebäude. Im Falle einer Dachkonstruktion kann dies das Gewicht von Personen sein, die Wartungsarbeiten auf dem Dach durchführen.
Die Werte der Nutzlast werden aus dem Eurocode EN 1991-1-1 Tabelle 6.2 (und dem nationalen Anhang) für die verschiedenen Kategorien von Belastungsbereichen wie Büro, Dach, Balkon, Treppenhaus, etc. entnommen.
Ich empfehle, die Norm oder unseren Artikel zur Nutzlast zu lesen, um ein besseres Verständnis zu bekommen. 📖📖
Wie wird jetzt die Nutzlast auf (Schräg-) Dächer angesetzt?
Lastrichtung
💡
Die Nutzlast auf dem Dach wird auf die gleiche Weise aufgebracht wie die Eigenlast. Z-Achse nach unten, wobei die Verteilung der Neigung des Daches folgt.
Nutzlast in 3D System
In diesem Beispiel verwenden wir 1,0 kN/m2 als charakteristische Nutzlast auf dem Dach. Dieser Wert kann im nationalen Anhang des Eurocodes nachgeschlagen werden und unterscheidet sich von Land zu Land.
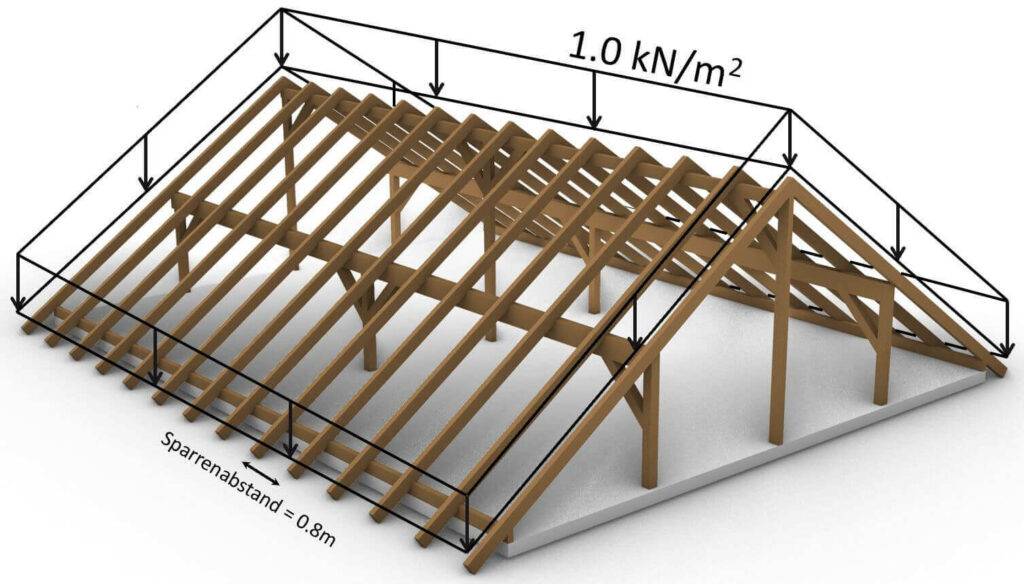
Nutzlast in 2D System
$$1.0 \frac{kN}{m^2} \cdot 0.8 m = 0.8 \frac{kN}{m^2} $$
Diese Linienlast kann jetzt auf das statische System angebracht werden.
5. Erdbebenlast
Die Erdbebenlast ist das Resultat eines Erdbebens.
Die Erdbebenlast wird mit dem Eurocode EN 1998 berechnet.
Leider habe ich nicht so viel Erfahrung mit Erdbebenlasten. Bisher hatte ich nur Projekte, bei denen ich die Erdbebenlast auf Flachdächer angebracht habe.
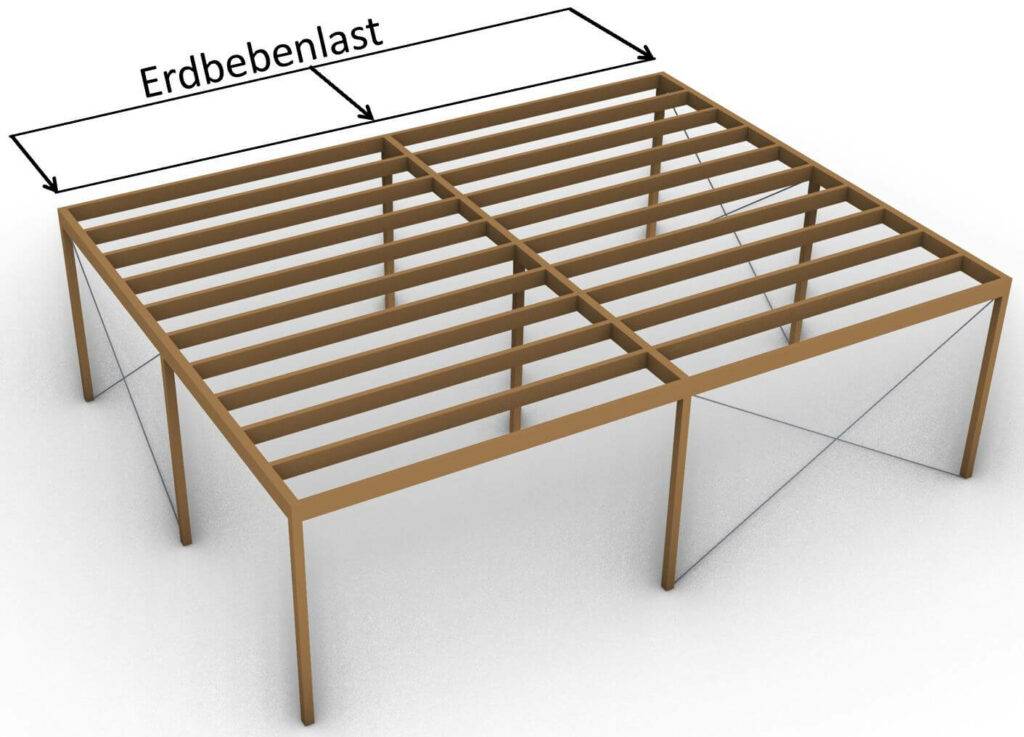
Lastrichtung
Bei Flachdächern wird die Erdbebenlast horizontal angebracht. Das Dach muss dieser Belastung standhalten und die Lasten zu aussteifenden Wänden oder Windverbänden leiten.
Hier ist auch ein gutes YouTube-Video, das die seismischen Lasten sehr gut erklärt.
Fazit
Nachdem du jetzt verstanden hast, welche Lasten man für ein Dach berücksichten muss und wie man diese berechnet, ist es jetzt an der Zeit Lastkombinationen aufzustellen.
👉👉 Wie stellt man Lastkombinationen auf? 👈👈
Sobald alle Lastfälle und -kombinationen festgelegt sind, können die statischen Elemente bemessen werden. Wir haben bereits viele Leitfäden über die Bemessung von Dachtragwerken geschrieben. 👇👇
Ich hoffe, dass dieser Artikel Dir geholfen hat, die Lasten auf Dächer zu verstehen. Falls Du noch Fragen hast, schreib in die Kommentare ✍️✍️.
Dachlasten FAQ
– Eigenlast
– Windlast
– Schneelast
– Nutzlast
– Erdbebenlast
Das Verständnis der Lasten auf einem Dach ist entscheidend, um sicherzustellen, dass es stabil und sicher ist. Eine unzureichende Berücksichtigung dieser Lasten kann zu Schäden am Dach oder sogar zur Gefährdung der Bewohner führen.
Es ist ratsam, einen Bauingenieur hinzuzuziehen, um Ihr Dach auf seine Tragfähigkeit in Bezug auf Schnee, Wind, Eigengewicht, Nutzlasten und Erdbebenlasten überprüfen zu lassen. Bauingenieure/Statiker können die notwendigen Berechnungen und Empfehlungen liefern.
![Schneelast Berechnung eines Flachdachs [2025]](https://www.structuralbasics.com/wp-content/uploads/2023/12/Schneelast-eines-Flachdachs-768x439.jpg)