Eigenlast – Was ist sie und wie berechnet man sie?

Kurzversion: Die Eigenlast ist das Eigengewicht aller Elemente eines Gebäudes oder eines Tragwerks, wie z.B. eines Betonträgers, eines Fußbodens oder des Daches. Die Eigenlast ist eine von vielen statischen Lasten, die bei der Statik berücksichtigt werden müssen.

Als Statiker berechne ich bei jedem Projekt Eigenlasten. Deswegen zeige ich in diesem Blogpost, was die Eigenlast ist, Beispiele für die Eigenlast und wie man die Eigenlast berechnet.

Falls du Video bevorzugst, kannst du auch unser YouTube Tutorial auf Englisch anschauen.

Lass uns starten. 🚀🚀

Was ist die Eigenlast?

Die Eigenlast ist eine ständige Last, die auf ein Gebäude einwirkt, wie z.B. das Eigengewicht von statischen Elementen (wie Betonplatten, Stahlträger oder Holzstützen) und nicht-statische Bauteile (wie der Dachaufbau, Fenster oder Fußböden). Das Gewicht wird berechnet und dann auf das statische Bauteil übertragen, das es trägt.

In der Statik ist dieses Gewicht – die Eigenlast – ein konstanter Faktor, um die Berechnung zu vereinfachen. Jedes Element in einem Gebäude trägt zur Eigenlast bei.

Wenn Du also ein Renovierungsprojekt durchführst und z. B. das Gewicht des Fußbodens erhöhst, solltest Du das mit einem Statiker besprechen, ob die Decke trotz der zusätzlichen Belastung standhält.

Berechnung der Eigenlast

Wie das Eigengewicht berechnet wird, hängt von dem Bauteil ab, das die Last aufnehmen muss.

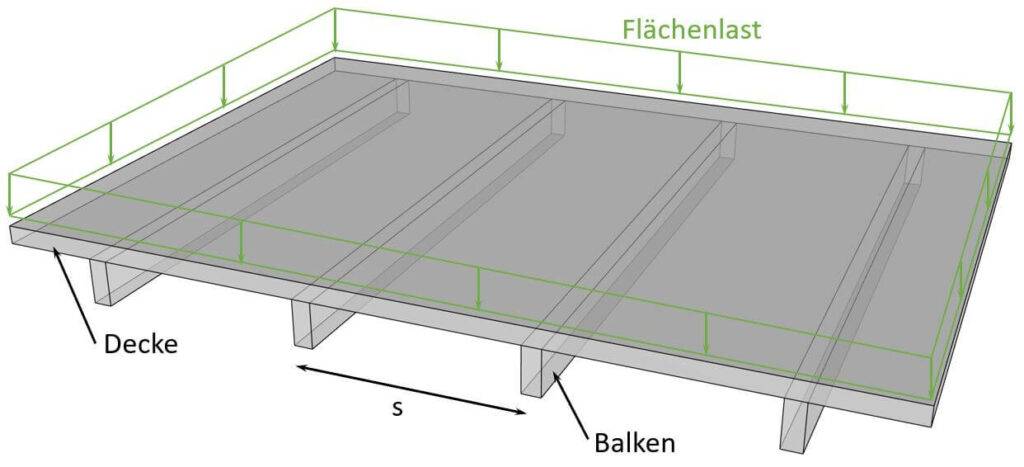
Zum Beispiel wird die Eigenlast einer Decke normalerweise als Flächenlast (kN/m²) berechnet, da die Decke selbst – ein statisches 2D-Element – die Last tragen muss.

Eigenlasten, die auf statische 1D-Elemente wie Balken, Stützen, Stäbe usw. wirken, sind in der Regel entweder Linienlasten (kN/m) oder Punktlasten (kN).

Schauen wir uns also an, wie man die verschiedenen Arten von Eigenlasten berechnet. 👇👇

Flächeneigenlast

Beispiel

Die Flächeneigenlast einer Betondecke mit einer Dichte von 2400 kg/m³ und einer Dicke von 18 cm wird folgendermaßen berechnet: 👇👇

$$g_k = 2400 \frac{kg}{m^3} \cdot 0.18m = 432 \frac{kg}{m^2} $$

Da wir Ingenieure die Statik nicht mehr mit kg rechnen, muss die Einheit von kg auf kN [Kilonewton] umgestellt werden.

Um kN zu erhalten, müssen wir das Ergebnis mit 0,0098 multiplizieren. Oder wenn wir etwas fauler sind, reicht in den meisten Fällen aus, das Ergebnis mit 0,01 zu multiplizieren.

$$g_k = 432 \frac{kg}{m^2} = 4.24 \frac{kN}{m^2}$$

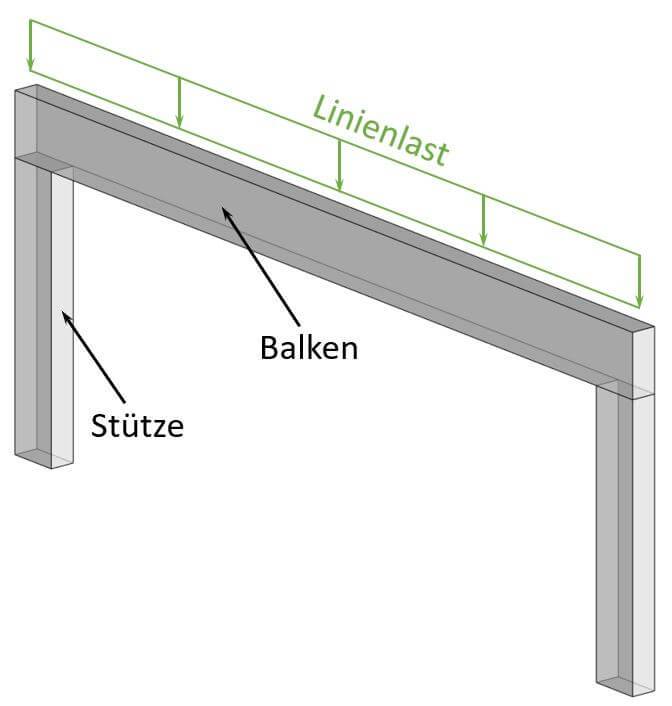
Linieneigenlast

Die Eigenlast wird als Linienlast für Balken verwendet.

Beispiel

Die Linienlast eines GL24h-Holzbalkens mit einer Dichte von 420 kg/m³, einer Querschnittsbreite von 10 cm und einer Querschnittshöhe von 20 cm wird wie folgt berechnet:

$$g_k = 420 \frac{kg}{m^3} \cdot 0.2m \cdot 0.1m = 8.4 \frac{kg}{m} $$

Wie bei der Flächenlast muss auch die Linienlast von kg in kN umgerechnet werden.

$$g_k = 8.4 \frac{kg}{m} = 0.08 \frac{kN}{m}$$

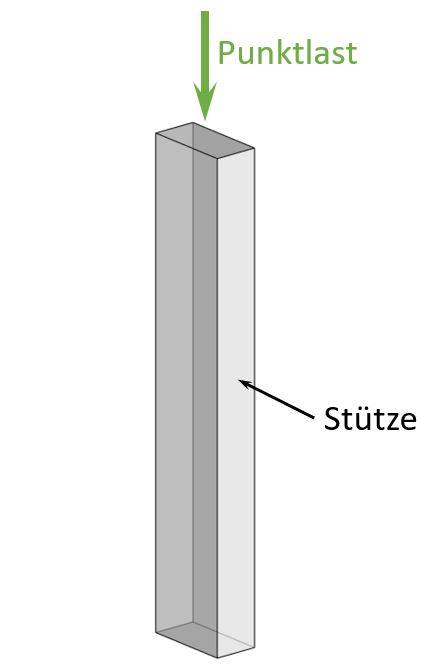
Punkteigenlast

Beispiel

Ein Beispiel, bei dem das Eigengewicht als Punktlast (kN) berechnet wird, sind Säulen. In diesem Fall berechnen wir also die Eigenlast einer Holzstütze.

Die Punkteigenlast einer GL24h-Säule mit einer Dichte von 420 kg/m³, einer Querschnittsbreite von 50cm, einer Querschnittshöhe von 50cm und einer Länge von 3m wird berechnet als:

$$g_k = 420 \frac{kg}{m^3} \cdot 0.5m \cdot 0.5m \cdot 3m = 315 kg $$

Wie bei der Linienlast muss auch die Punktlast von kg in kN umgerechnet werden.

$$g_k = 315 kg = 3.1 kN$$

Beispiel Berechnung der Eigenlast eines Bodenaufbaus

In diesem Abschnitt zeige ich, wie ich als Statiker die Eigenlast eines Bodens berechne. Die Bodenschichten werden normalerweise vom Architekten vorgegeben.

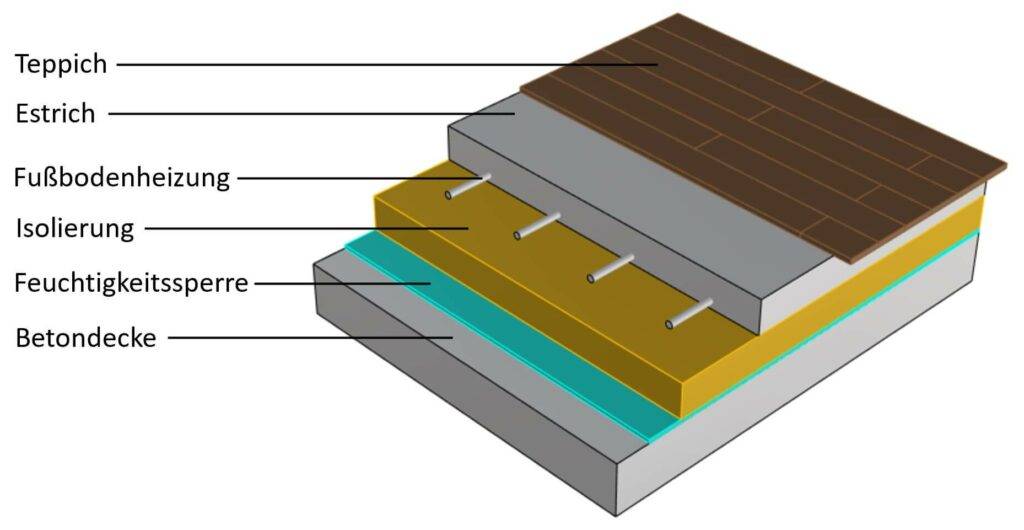
Um die Eigenlast der einzelnen Schichten zu berechnen, empfehle ich, entweder die Dichte des Materials zu googeln oder zu prüfen, ob die Produktseite bzw. das Produkt Datenblatt sein Gewicht angibt.

Beim Googeln habe ich zum Beispiel herausgefunden, dass die Dichte von Rockwool-Isolierungen zwischen 22 kg/m³ und 1000 kg/m³ variiert. Suche Dir also ein bestimmtes Produkt aus und ermittel seine Dichte. Oder wenn Du noch nicht weißt, welches Produkt Du verwenden wirst, ist es immer eine gute Idee, 3 Werte von verschiedenen Herstellern zu finden und die höchste Dichte in der Berechnung zu verwenden.

Man berechnet das Eigengewicht für jede Schicht einzeln und addiert dann die Werte, um die Flächeneigenlast zu erhalten, dass man dann auf die Decke aufbringen muss.

Bodenschicht	Dicke [mm]	Dichte [kg/m3]	Flächenlast [kN/m2]
Betondecke	200	2400	4.71
Isolierung	200	42	0.39
Estrich	200	1000	1.96
Bodenbelag	15	660	0.1
Summe			7.16

Beispielelemente für die man die Eigenlast berechnet

Hier sind einige Beispiele für Baumaterialien, die bei der Statik als Eigenlast berücksichtigt werden müssen:

• Gebäude Ausrüstung
• Treppen
• Stahl-, Beton- und Holzbalken
• Aufzüge
• Glasfenster und -paneele
• Fassadenelemente
• Decken aus Holz und Beton
• Isolierung
• Dachaufbau
• Ziegel
• Lüftungskanäle
• Stahl-, Beton- und Holzsäulen
• Heizungsanlagen
• Sonnenkollektoren
• Garagenrampen
• usw.

Um nur ein paar zu nennen. 😎😎

Wie bereits oben erläutert, muss je nachdem, an welchem Bauteil das Bauelement befestigt ist bzw. von welchem Element es getragen wird, eine Flächen-, Linien- oder Punktlast aus der Dichte berechnet werden.

Wie schon oben genannt wird, in einigen Produkthandbüchern angegeben, wie viel das Element wiegt.

Richtung der Eigenlast

Nachdem wir nun wissen, wie man die Eigenlast und ihre verschiedenen Typen berechnet, müssen wir noch verstehen, wie man sie auf statische Elemente ansetzt.

In den meisten Fällen wird das Eigengewicht auf ein horizontales Element wie z. B. eine Decke, einen Balkon, ein Flachdach oder eine Treppe aufgebracht.

In diesem Fall kann das Eigengewicht einfach vertikal aufgebracht werden, wie in der nächsten Abbildung, wo eine Geschossdecke an drei Kanten von Wänden getragen wird.

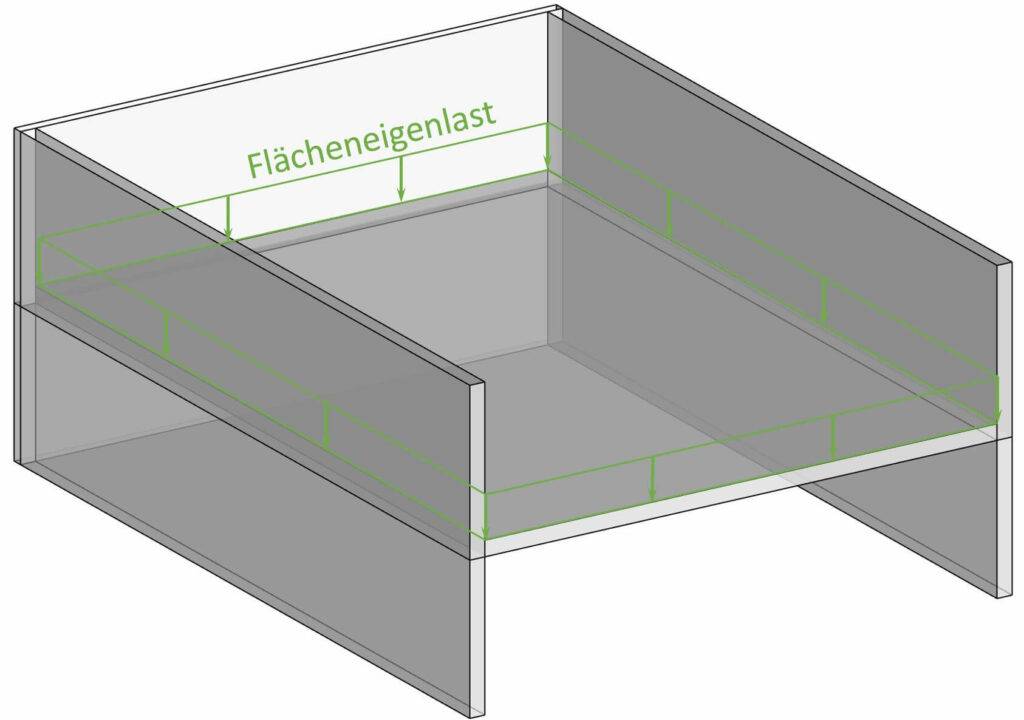
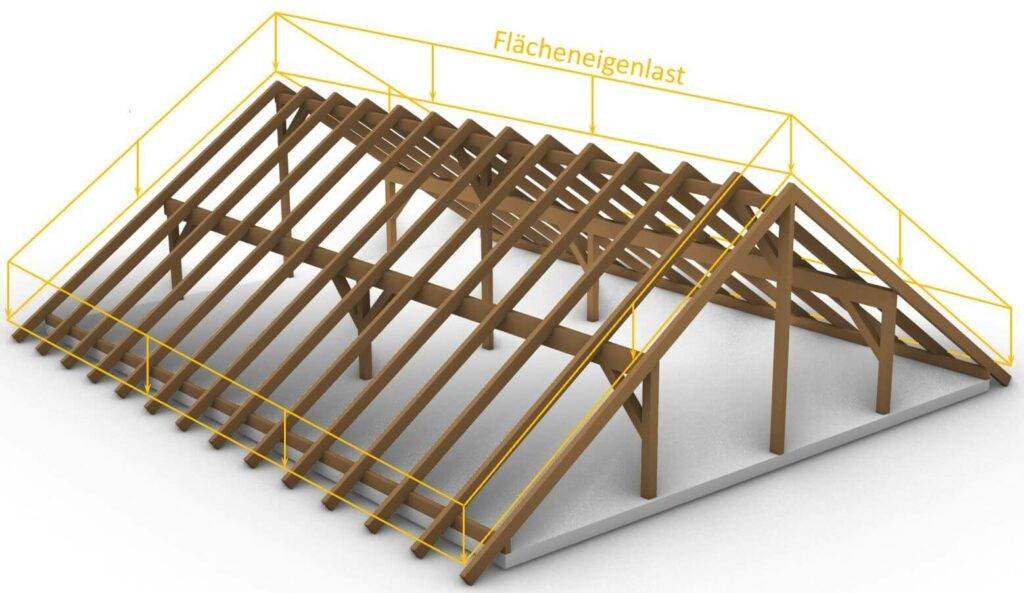
Es wird etwas komplizierter, wenn wir die Eigenlast auf ein geneigtes Bauteil wie ein Sparrendach aufbringen müssen. Wir haben einen ausführlichen Artikel über Lasten auf Dächern geschrieben, den Du hier nachlesen kannst.

Aber hier die Kurzfassung: Die Eigenlast wird wie die Nutzlast auf geneigte Tragwerke aufgebracht.

Die Lastrichtung ist die z-Achse nach unten ⬇️⬇️, während die Verteilung der Neigung des Daches folgt.

Einheit

Die Einheit der Eigenlast in Europa ist vom statischen Element abhängig. Die Eigenlast wird mit einer der folgenden Einheiten gerechnet

• Flächenlast: kN/m² = Kilonewton per Quadratmeter
• Linien/Streckenlast: kN/m = Kilonewton per Meter
• Punktlast: kN = Kilonewton

Fazit

Nachdem du nun verstanden hast, was die Eigenlast ist, wie man sie berechnet und wie sie verwendet wird, ist es an der Zeit, andere Lasten, die in der Statik verwendet werden, kennenzulernen: 👇👇

• Schneelast
• Windlast

Auf statische Elemente wirken immer mehrere Lasten ein. Die Berücksichtigung dieser verschiedenen Lasten bei der Tragwerksplanung erfolgt durch Lastkombinationen mit Sicherheitsfaktoren.

Sobald dann alle Lasten und Lastkombinationen eingerichtet sind, können die Tragwerkselemente dimensioniert und nachgewiesen werden. Wir haben bereits viele Anleitungen zur Bemessung von Tragelementen geschrieben. 👇👇

• Bemessung eines Holzbalkens
• Statik eines Pfettendachs
• Bemessung einer Holzstütze

Ich hoffe, dass dir dieser Artikel geholfen hat, die Eigenlast zu verstehen. Falls du noch Fragen hast: Lass es uns in den Kommentaren wissen. ✍️✍️