Concrete And Reinforcement Properties For Structural Design {Introduction}

This is a quick introduction of the main concrete and reinforcement properties I use – as a structural engineer – to design reinforced concrete beams like the compression strength of concrete, partial safety factors and tensile strength of reinforcement.

These material properties are the fundamentals of structural design.

In this article, I’ll explain what properties are important, where you find them and how to calculate them (if needed).

Let’s get into it.

The 5 Most Important Concrete Properties

Material properties of concrete and reinforcement are really important for structural design because they define the resistance of the material like compression or tension resistance.

The resistance or strength properties of concrete are defined in EN 1992-1-1 Table 3.1. We’ll summarize it for you below.

In general, concrete has different strength classes, which are categorized by their compression strength. For example, a concrete with the compressive strength of 30 MPa is named a C30 concrete.

1. Partial safety factor γ_c

The value of the partial safety factor can be found in EN 1992-1-1 Table 2.1N. For ULS load combinations, this value is defined as:

And for accidental loads as:

Note that these values are usually defined differently in the National Annex. Make sure to check it.

The partial safety factor is used to calculate the design resistance from the characteristic resistance/strength values, which we’ll define in the next sections.

In general (for all materials) we calculate the design resistance with EN 1990 (6.6c):

With R_k as the characteristic resistance and γ_M the partial safety factor. In our case, that would be γ_c.

2. Compression strength

f_ck is the characteristic compressive cylinder strength of concrete at 28 days. The values are determined with tests and statistical methods.

The values of f_ck are defined in EN 1992-1-1 Table 3.1. As said earlier, the strength class is named after the characteristic compressive strength. A C25 concrete has a compressive strength of 25 MPa.

Here’s an overview of the values of f_ck of the different strength classes.

Strength class	Compressive strength fck [MPa]
C12	12
C16	16
C20	20
C25	25
C30	30
C35	35
C40	40
C45	45
C50	50
C55	55
C60	60
C70	70
C80	80
C90	90

The compressive strength is used in almost every structural design verification of reinforced concrete. Here are a few examples:

• Compression verification
• Bending verification
• Shear verification

3. Tensile strength f_ctm

f_ctm is the mean value of the axial tensile strength of concrete.

We’ll find the values of f_ctm in EN 1992-1-1 Table 3.1. Here’s an overview of the different strength classes.

Strength class	Mean value of the axial tensile strength fctm [MPa]
C12	1.6
C16	1.9
C20	2.2
C25	2.6
C30	2.9
C35	3.2
C40	3.5
C45	3.8
C50	4.1
C55	4.2
C60	4.4
C70	4.6
C80	4.8
C90	5.0

The tensile strength is also used in many structural design verifications. Here are a few examples:

• Minimum reinforcement requirement
• Bending verification
• Shear verification at the interface between 2 concrete casts at different times

4. E-modulus E_cm

E_cm is the secant modulus of elasticity of concrete. The E-modulus E_cm is calculated as:

With,

• f_cm as the mean value of the concrete cylinder compressive strength. The value for f_cm can also be found in EN 1992-1-1 Table 3.1.

Or, we’ll find the values of E_cm in EN 1992-1-1 Table 3.1. Here’s an overview of the different strength classes.

Strength class	Secant modulus of elasticity fcm [GPa]
C12	27
C16	29
C20	30
C25	31
C30	33
C35	34
C40	35
C45	36
C50	37
C55	38
C60	39
C70	41
C80	42
C90	44

The E-modulus is used in the crack width calculation of rc beams and slabs.

5. Concrete cover c

The concrete cover is the closest distance between the edge of the concrete element and the reinforcement.

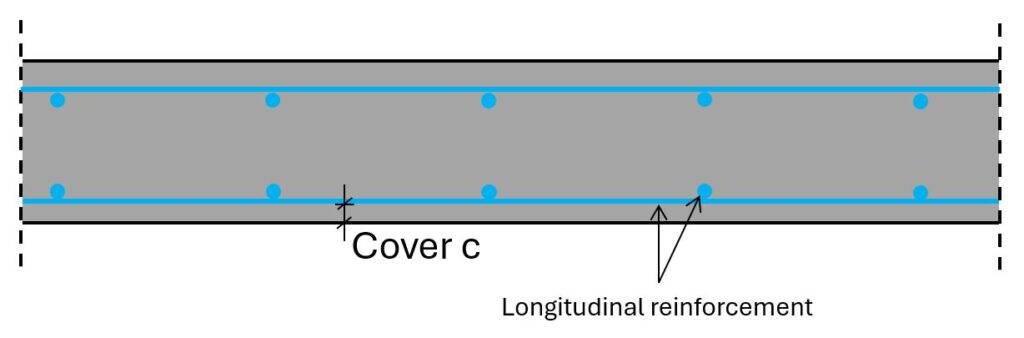
The cover is used to protect the reinforcement from external influences, which could damage the reinforcement, like water or fire.

Where,

• c_min = minimum cover according to EN 1992-1-1 4.4.1.2
• Δc_dev = allowance in design for deviation according to 4.4.1.3

Now, we won’t dive deep into how to calculate c_min and define Δc_dev, because it’s an article itself. And most countries have the minimum values defined in textbooks for the different reinforced concrete elements, concrete types and environmental conditions.

These were the 5 most important concrete properties. Of course these were not all, but the main ones I use in my job as a structural engineer.

The 3 Most Important Reinforcement Properties

The second material that is part of reinforced concrete is reinforcing steel or reinforcement.

Here are the 3 main properties of reinforcement, where they are defined and in what verifications they are used.

1. Partial safety factor γ_s

The value of the partial safety factor can be found in EN 1992-1-1 Table 2.1N. For ULS load combinations, this value is defined as:

And for accidental loads as:

2. Yield strength f_y (=tensile strength)

f_y.k is the characteristic yield strength of reinforcement.

The 2 most common characteristic yield strengths are either 500 MPa or 550 MPa.

Rebar type	Yield strength fy.k [MPa]
B500B	500
B550B	550

The tensile strength is used in the following structural design verifications:

• Minimum reinforcement requirement
• Cracking verification
• Bending verification
• Shear verification
• Tension verification
• etc.

3. E-modulus E_s

E_s is the modulus of elasticity of the reinforcing steel.

The E-modulus E_s of reinforcement is defined as:

The E-modulus is used in the following structural design verifications:

• Calculation of the neutral axis of a cracked rc section
• Column design
• Cracking verification
• etc.

Final Words

As mentioned earlier, the concrete and reinforcement properties of a rc element are the starting point of any structural design.

Once set up, you can start calculating the internal forces and after that design the structural element like:

• Reinforced concrete beams
• Reinforced concrete columns
• Flat slabs or
• Shear walls